早教吧作业答案频道 -->数学-->
如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1.(1)求证:△DMN∽△BCN;(2)求BD的长;(3)若△DCN的面积为2,求四边形ABNM的面积.
题目详情
如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1.
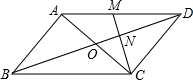
(1)求证:△DMN∽△BCN;
(2)求BD的长;
(3)若△DCN的面积为2,求四边形ABNM的面积.

(1)求证:△DMN∽△BCN;
(2)求BD的长;
(3)若△DCN的面积为2,求四边形ABNM的面积.
▼优质解答
答案和解析
(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DMN=∠BCN,∠MDN=∠NBC,
∴△DMN∽△BCN;
(2)∵△DMN∽△BCN,
∴
=
,
∵M为AD中点,
∴MD=
AD=
BC,
即
=
,
∴
=
,即BN=2DN,
设OB=OD=x,则有BD=2x,BN=OB+ON=x+1,DN=x-1,
∴x+1=2(x-1),
解得:x=3,
∴BD=2x=6;
(3)∵△MND∽△CNB,且相似比为1:2,
∴MN:CN=DN:BN=1:2,
∴S△MND=
S△CND=1,S△BNC=2S△CND=4.
∴S△ABD=S△BCD=S△BCN+S△CND=4+2=6,
∴S四边形ABNM=S△ABD-S△MND=6-1=5.
∴AD∥BC,
∴∠DMN=∠BCN,∠MDN=∠NBC,
∴△DMN∽△BCN;
(2)∵△DMN∽△BCN,
∴
| MD |
| CB |
| DN |
| BN |
∵M为AD中点,
∴MD=
| 1 |
| 2 |
| 1 |
| 2 |
即
| MD |
| CB |
| 1 |
| 2 |
∴
| DN |
| BN |
| 1 |
| 2 |
设OB=OD=x,则有BD=2x,BN=OB+ON=x+1,DN=x-1,
∴x+1=2(x-1),
解得:x=3,
∴BD=2x=6;
(3)∵△MND∽△CNB,且相似比为1:2,
∴MN:CN=DN:BN=1:2,
∴S△MND=
| 1 |
| 2 |
∴S△ABD=S△BCD=S△BCN+S△CND=4+2=6,
∴S四边形ABNM=S△ABD-S△MND=6-1=5.
看了 如图,在平行四边形ABCD中...的网友还看了以下:
在三角形ABC中,角A,B,C所对的边分别为a,b,c,已知A=2B,sinB=根号3/3,(1) 2020-04-05 …
已知三角形ABC,角ABC的对边是abc,向量m=(a,b),向量n=(sinB,2si已知三角形 2020-05-16 …
一道关于集合的高中数学题A={x|-2≤x≤a} B={y|y=2x+3,x∈A} M={z|z= 2020-05-16 …
在三角形ABC中,角A,B,C的对边分别为a,b,c,且满足asinC=根3ccosA,AB*AC 2020-05-17 …
已知三角形ABC,边b=4,c=3,B=60°求边a和三角形ABC的面积 2020-05-23 …
在三角形ABC中,若A=60度,a=7,b=5,求边c 2020-07-19 …
已知G是△ABO的重心,M是边AB的中点已知点G是△ABO的重心,M是AB边的中点(1)求向量GA 2020-07-22 …
已知不等式x^2+(a-1)x-a大于0的解集为A,不等式(x+a)(x+b)小于等于0的解集为B 2020-07-30 …
已知线段a,b,m,求做三角形ABC,使AB=a,AC=b,且BC边上的中线AD=m. 2020-12-05 …
在△ABC中,已知a=3倍的根号3,c=2,B=150°,求边b的长及△ABC的面积S△. 2021-02-07 …