早教吧作业答案频道 -->数学-->
如图,在△ABC中,AB=AC=10,BC=16,点D是边BC上一动点(不与B,C重合),∠ADE=∠B,DE交AC于点E.(1)求证:△ADE∽△ACD;(2)若△DCE为直角三角形,求线段BD的长;(3)求线段CE长的取值范
题目详情
如图,在△ABC中,AB=AC=10,BC=16,点D是边BC上一动点(不与B,C重合),∠ADE=∠B,DE交AC于点E.
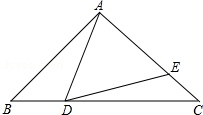
(1)求证:△ADE∽△ACD;
(2)若△DCE为直角三角形,求线段BD的长;
(3)求线段CE长的取值范围.(直接写出答案)

(1)求证:△ADE∽△ACD;
(2)若△DCE为直角三角形,求线段BD的长;
(3)求线段CE长的取值范围.(直接写出答案)
▼优质解答
答案和解析
(1)证明:∵AB=AC,
∴∠B=∠C,
又∵∠ADE=∠B,
∴∠ADE=∠C,
∵∠DAE=∠CAD,
∴△ADE∽△ACD;
(2)△DCE为直角三角形,有以下两种可能:①∠CED=90°②∠EDC=90°.
①当∠CED=90°时,即∠AED=90°,由①可知:△ADE∽△ACD,
∴∠ADC=∠AED,
∵∠AED=90°,
∴∠ADC=90°,即AD⊥BC,
∵AB=AC,
∴BD=CD,
∴BD=8.
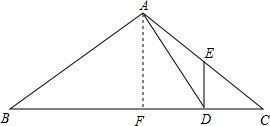 ②当∠EDC=90°时,
②当∠EDC=90°时,
∵∠ADE+∠EDC=∠B+∠BAD,∠ADE=∠B,
∴∠BAD=∠EDC=90°,
如图,过A作AF⊥BC于F,则BF=8,
∵∠B是公共角,∠AFB=∠BAD=90°,
∴△BFA∽△BAD,
∴
=
,
∴
=
,
∴BD=
.
综上所述,△DCE为直角三角形时,BD=8或BD=
.
(3)由(2)得:∠EDC=∠BAD,
∵∠B=∠C,
∴△CDE∽△BAD,
设BD=y,CE=x,
∴
=
,
∴
=
,
整理得:y2-16y+64=64-10x,
即(y-8)2=64-10x,
∵0<BD<16,
∴0<x≤6.4.
∴∠B=∠C,
又∵∠ADE=∠B,
∴∠ADE=∠C,
∵∠DAE=∠CAD,
∴△ADE∽△ACD;
(2)△DCE为直角三角形,有以下两种可能:①∠CED=90°②∠EDC=90°.
①当∠CED=90°时,即∠AED=90°,由①可知:△ADE∽△ACD,
∴∠ADC=∠AED,
∵∠AED=90°,
∴∠ADC=90°,即AD⊥BC,
∵AB=AC,
∴BD=CD,
∴BD=8.
 ②当∠EDC=90°时,
②当∠EDC=90°时,∵∠ADE+∠EDC=∠B+∠BAD,∠ADE=∠B,
∴∠BAD=∠EDC=90°,
如图,过A作AF⊥BC于F,则BF=8,
∵∠B是公共角,∠AFB=∠BAD=90°,
∴△BFA∽△BAD,
∴
| AB |
| BD |
| BF |
| AB |
∴
| 10 |
| BD |
| 8 |
| 10 |
∴BD=
| 25 |
| 2 |
综上所述,△DCE为直角三角形时,BD=8或BD=
| 25 |
| 2 |
(3)由(2)得:∠EDC=∠BAD,
∵∠B=∠C,
∴△CDE∽△BAD,
设BD=y,CE=x,
∴
| AB |
| DC |
| BD |
| CE |
∴
| 10 |
| 16-y |
| y |
| x |
整理得:y2-16y+64=64-10x,
即(y-8)2=64-10x,
∵0<BD<16,
∴0<x≤6.4.
看了 如图,在△ABC中,AB=A...的网友还看了以下:
满足{a}⊆M⊆{a,b,c,d}的集合M的个数是( ) 是{a} {a,b} {a,c} {a, 2020-04-05 …
若非空集合M⊆N={a,b,c,d},则M的个数为8个{a},{b},{c},{d},{a,b}, 2020-05-15 …
设a、b、c分别是△ABC中∠A、∠B、∠C所对边的边长,则直线xsinA+ay+c=0与bx-y 2020-05-19 …
设a、b、c分别是△ABC中∠A、∠B、∠C所对边的边长,则直线xsinA+ay+c=0与bx-y 2020-05-19 …
______表示了对象间“is part of”的关系。A.联合B.引用C.组合D.继承A.B.C. 2020-05-26 …
______表示了对象间“is-a”的关系。A.组合B.引用C.聚合D.继承A.B.C.D. 2020-05-26 …
______表示了对象间“is member of”的关系。A.联合B.引用C.聚合D.继承A.B. 2020-05-26 …
已知集合A={正方体},B={长方体},C={正四棱柱},D={直四棱柱},E={棱柱},F={直 2020-06-27 …
有abcd四个齿轮,a咬合b,b咬合c,c咬合d,这四个齿轮齿数比是3:4:5:6,当ad一共转动 2020-07-01 …
C语言赋值问题38.下列语句中符合C语言的赋值语句是(D).A.a=7+b+c=a+7;B.a=7+ 2020-12-31 …