早教吧作业答案频道 -->数学-->
如图所示,P、Q分别是Rt△ABC两直角边AB、AC上两点,M为斜边BC的中点,且PM⊥QM,MD⊥AB于点D,ME⊥AC于点E.求证:(1)△MPD∽△MQE;(2)AD•PD=AE•EQ:(3)PB2+QC2=PM2+QM2.
题目详情
如图所示,P、Q分别是Rt△ABC两直角边AB、AC上两点,M为斜边BC的中点,且PM⊥QM,MD⊥AB于点D,ME⊥AC于点E.求证:
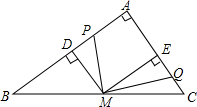
(1)△MPD∽△MQE;
(2)AD•PD=AE•EQ:
(3)PB2+QC2=PM2+QM2.

(1)△MPD∽△MQE;
(2)AD•PD=AE•EQ:
(3)PB2+QC2=PM2+QM2.
▼优质解答
答案和解析
证明:(1)∵MD⊥AB于点D,ME⊥AC,∠A=90°,
∴∠MDP=∠MEA=∠A=90°,
∴四边形ADME是矩形,
∴AD=EM,AE=DM,∠DME=90°,
∵PM⊥QM,
∴∠PMQ=90°,
∴∠DMP=∠EMQ,
∴△MPD∽△MQE;
(2)∵△MPD∽△MQE,
∴
=
,
∵AD=EM,AE=DM,
∴
=
,
∴AD•PD=AE•EQ;
(3)如图,以M点为中心,△MCQ顺时针旋转180°至△MBN,
∴△MCQ≌△MBN,
∴BN=QC,MN=MQ,∠MBN=∠C,
连接PN,PQ,
∵PM⊥QM,
∴PM垂直平分NQ,
∴PN=PQ,
∵△ABC是直角三角形,BC是斜边,
∴∠ABC+∠C=90°,
∴∠ABC+∠MBN=90°,
即△PBN是直角三角形,
根据勾股定理可得,PN2=PB2+BN2,
∴PQ2=PB2+QC2,
∵PQ2=PM2+QM2,
∴PB2+QC2=PM2+QM2.
∴∠MDP=∠MEA=∠A=90°,
∴四边形ADME是矩形,
∴AD=EM,AE=DM,∠DME=90°,
∵PM⊥QM,
∴∠PMQ=90°,
∴∠DMP=∠EMQ,
∴△MPD∽△MQE;
(2)∵△MPD∽△MQE,
∴
| PD |
| EQ |
| DM |
| EM |

∵AD=EM,AE=DM,
∴
| PD |
| EQ |
| AE |
| AD |
∴AD•PD=AE•EQ;
(3)如图,以M点为中心,△MCQ顺时针旋转180°至△MBN,
∴△MCQ≌△MBN,
∴BN=QC,MN=MQ,∠MBN=∠C,
连接PN,PQ,
∵PM⊥QM,
∴PM垂直平分NQ,
∴PN=PQ,
∵△ABC是直角三角形,BC是斜边,
∴∠ABC+∠C=90°,
∴∠ABC+∠MBN=90°,
即△PBN是直角三角形,
根据勾股定理可得,PN2=PB2+BN2,
∴PQ2=PB2+QC2,
∵PQ2=PM2+QM2,
∴PB2+QC2=PM2+QM2.
看了 如图所示,P、Q分别是Rt△...的网友还看了以下:
变成要经过m次衰变、n次衰变,中子数减少的个数为q,则A.m=8,n=6,q=32B.m=6,n= 2020-04-05 …
下列各题中,p是q的什么条件?(1)p:a+b=0,q:a*2+b*2=0;(2)p:四边形的对角 2020-04-09 …
[20分][高一不等式]已知a,b,m,n∈R+,设p=Sqrt(ab)+Sqrt(cd),q=S 2020-05-23 …
2014届初三数学模拟测试卷(2)第25题已知点A(m,n),B(p,q)(m<p)在直线y=kx 2020-06-30 …
6、如果四个互不相同的正整数m,n,p,q满足(6-m)(6-n)(6-p)(6-q)=4,那么m 2020-07-19 …
很难得数学题设A交集B=∅,m={P|P⊆A},N={Q|Q⊆B},则()A.M∩N=∅B.M∩N 2020-07-30 …
因式分解急!1.a(m+n)-b(m+n)⒉xy(a-b)+x(a-b)3.n(x+y)+x+y⒋a 2020-11-03 …
(2014•江门一模)设a,b∈R,定义运算“⊗”和“⊕”如下:a⊗b=a,a≤bb,a>b,a⊕b 2020-11-12 …
有这么一道题(截取下来的):q是质数,1/q+2/q+...+(q-1)/q=m为什么答案分析那里写 2020-11-20 …
由Q吸=cm(t-t0)导出c=Q吸m(t-t0),下列说法正确的是()A.c和Q吸成正比B.c和m 2020-11-29 …