早教吧作业答案频道 -->数学-->
如图,已知等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=CD=2,点E在BC边上,AE与BD交于点F,∠BAE=∠DBC.(1)求证:△ABE∽△BCD;(2)求tan∠DBC的值;(3)求线段BF的长.
题目详情
如图,已知等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=CD=2,点E在BC边上,AE与BD交于点F,∠BAE=∠DBC.
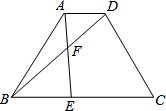
(1)求证:△ABE∽△BCD;
(2)求tan∠DBC的值;
(3)求线段BF的长.

(1)求证:△ABE∽△BCD;
(2)求tan∠DBC的值;
(3)求线段BF的长.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD为等腰梯形,
∴∠ABE=∠C,且∠BAE=∠DBC,
∴△ABE∽△BCD;
(2) 过D作DG⊥BC于点G,
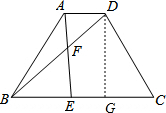
∵AD=1,BC=3,
∴CG=
(BC-AD)=1,BG=2,
又∵在Rt△DGC中,CD=2,CG=1,
∴DG=
,
在Rt△BDG中,tan∠DBC=
=
;
(3) 由(2)在Rt△BGD中,由勾股定理可求得BD=
,
由(1)△ABE∽△BCD可得
=
,即=
=
,解得BE=
,
又∵AD∥BC,
∴
=
,且DF=BD-BF,
∴
=
,
解得BF=
.
∴∠ABE=∠C,且∠BAE=∠DBC,
∴△ABE∽△BCD;
(2) 过D作DG⊥BC于点G,

∵AD=1,BC=3,
∴CG=
| 1 |
| 2 |
又∵在Rt△DGC中,CD=2,CG=1,
∴DG=
| 3 |
在Rt△BDG中,tan∠DBC=
| DG |
| BG |
| ||
| 2 |
(3) 由(2)在Rt△BGD中,由勾股定理可求得BD=
| 7 |
由(1)△ABE∽△BCD可得
| AB |
| BC |
| BE |
| CD |
| BE |
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
又∵AD∥BC,
∴
| AD |
| BE |
| DF |
| BF |
∴
| 1 | ||
|
| ||
| BF |
解得BF=
4
| ||
| 7 |
看了 如图,已知等腰梯形ABCD中...的网友还看了以下:
当地壳板块发生张裂时,地表会产生什么现象()A.形成盆地或丘陵B.形成高大的山脉C.形成裂谷或海洋 2020-05-14 …
细菌度过不良环境的方式是()A.形成孢子B.大量繁殖C.形成芽孢D.形成荚膜 2020-05-14 …
有氧呼吸过程中产生能量最多的是()A.形成二氧化碳时B.形成[H]时C.形成水时D.形成丙酮酸时 2020-05-14 …
双子叶植物的茎的木质部比韧皮部发达的原因是()A.木质部细胞生长快B.形成层向内分裂产生的细胞多C 2020-06-21 …
多年生的木质茎,越靠近髓部的木质部()A.形成的越早B.形成的越晚C.形成的有早有晚D.形成的时间 2020-07-01 …
下列各种说法中正确的是()A.极性键只能形成极性分子B.CO2中碳原子是sp2杂化C.形成配位键的 2020-07-11 …
5.从图中不同纬度海陆水平衡的差异可以推断出()A.形成陆地降水的水汽主要来自中低纬度海洋B.形成海 2020-11-03 …
下列()是引用调用11、下列()是引用调用。A.形参是指针,实参是地址值B.形参和实参都是变量C.形 2020-11-11 …
(2013•柳州)如图是经过轴对称变换后所得的图形,与原图形相比()A.形状没有改变,大小没有改变B 2020-11-13 …
如图是“某地水循环运动中的水量平衡示意图”.读图完成第23~24题.图中M表示()A.形成地下水B. 2020-11-26 …