早教吧作业答案频道 -->物理-->
如图所示,在以O1点为圆心且半径为r=0.10m的圆形区域内,存在着竖直向下、场强大小为E=43×105V/m的匀强电场(图中未画出).圆的左端跟y轴相切于直角坐标系原点O,右端与一个足够大的荧
题目详情
如图所示,在以O1点为圆心且半径为r=0.10m的圆形区域内,存在着竖直向下、场强大小为E=4
×105 V/m的匀强电场(图中未画出).圆的左端跟y轴相切于直角坐标系原点O,右端与一个足够大的荧光屏MN相切于x轴上的A点.一比荷
=1.0×108 C/kg的带正电粒子从坐标原点O沿x轴正方向入射,粒子重力不计.
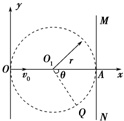
(1)若粒子在圆形区域的边界Q点射出匀强电场区域,O1A与O1Q之间的夹角为θ=60°,求粒子从坐标原点O入射的初速度v0;
(2)撤去电场,在该圆形区域内加一磁感应强度大小为B=0.15T、方向垂直纸面向里的匀强磁场,且将该圆形磁场以过O点并垂直于纸面的直线为轴,逆时针缓慢旋转90°,在此过程中不间断地射入题干中所述粒子,粒子入射的速度等于(1)中求出的v0,求在此过程中打在荧光屏MN上的粒子与A点的最远距离.
| 3 |
| q |
| m |

(1)若粒子在圆形区域的边界Q点射出匀强电场区域,O1A与O1Q之间的夹角为θ=60°,求粒子从坐标原点O入射的初速度v0;
(2)撤去电场,在该圆形区域内加一磁感应强度大小为B=0.15T、方向垂直纸面向里的匀强磁场,且将该圆形磁场以过O点并垂直于纸面的直线为轴,逆时针缓慢旋转90°,在此过程中不间断地射入题干中所述粒子,粒子入射的速度等于(1)中求出的v0,求在此过程中打在荧光屏MN上的粒子与A点的最远距离.
▼优质解答
答案和解析
(1)由题意可知,该粒子将在匀强电场中做类平抛运动,设其在电场中的运动时间为t,粒子在电场中运动的加速度大小为a,则有:
r+rcosθ=v0t,
rsinθ=
at2,
qE=ma,
以上三式联立可得:v0=(1+cosθ)
,
代入数据解得:v0=3×106 m/s.
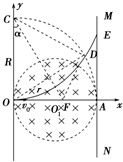 (2)由题意可知,粒子在匀强磁场中做匀速圆周运动的轨道半径为:R=
(2)由题意可知,粒子在匀强磁场中做匀速圆周运动的轨道半径为:R=
=0.2m,
以O点为圆心、OA=0.2m为半径做出圆弧AC交y轴于C点,
以C点为圆心、CO为半径作出粒子运动的轨迹交弧AC于D点,
则OD=2r=0.2m,如图所示,过D点作切线,分别交OA于F点,交MN于E点,
则E点即粒子能够打在荧光屏MN上的粒子离A点的最远距离,
由几何关系可知:sinα=
,
所以:OF=Rtanα,
因此AF=2r-OF,
由几何关系可知∠EFA=2α,
所以AE=AFtan2α,
以上各式联立解得:AE=
m.
答:(1)粒子从坐标原点O入射的初速度v0为3×106m/s;
(2)在此过程中打在荧光屏MN上的粒子与A点的最远距离为
m.
r+rcosθ=v0t,
rsinθ=
| 1 |
| 2 |
qE=ma,
以上三式联立可得:v0=(1+cosθ)
|
代入数据解得:v0=3×106 m/s.
 (2)由题意可知,粒子在匀强磁场中做匀速圆周运动的轨道半径为:R=
(2)由题意可知,粒子在匀强磁场中做匀速圆周运动的轨道半径为:R=| mv0 |
| qB |
以O点为圆心、OA=0.2m为半径做出圆弧AC交y轴于C点,
以C点为圆心、CO为半径作出粒子运动的轨迹交弧AC于D点,
则OD=2r=0.2m,如图所示,过D点作切线,分别交OA于F点,交MN于E点,
则E点即粒子能够打在荧光屏MN上的粒子离A点的最远距离,
由几何关系可知:sinα=
| r |
| R |
所以:OF=Rtanα,
因此AF=2r-OF,
由几何关系可知∠EFA=2α,
所以AE=AFtan2α,
以上各式联立解得:AE=
| ||
| 5 |
答:(1)粒子从坐标原点O入射的初速度v0为3×106m/s;
(2)在此过程中打在荧光屏MN上的粒子与A点的最远距离为
| ||
| 5 |
看了 如图所示,在以O1点为圆心且...的网友还看了以下:
已知椭圆x^2/4+y^/3=1,F为右焦点,M为椭圆上一点,以M为圆心,MF为半径作圆M,问点M 2020-04-27 …
数学圆与直线的一道题已知圆O:x^2+y^2=1和点M(4,2)(1)求以点M为圆心,且被直线y= 2020-04-27 …
已知椭圆C:的离心率为,F1、F2分别为椭圆C的左、右焦点,若椭圆C的焦距为2.(1)求椭圆C的方 2020-05-15 …
已知椭圆C:x2a2+y2b2=1(a>b>0)的左、右焦点分别为F1(-1,0)、F2(1,0) 2020-06-21 …
已知圆M(M为圆心)的方程为x2+(y-2)2=1,直线l的方程为x-2y=0,点P在直线l上,过 2020-07-26 …
已知圆O:x²+y²=1和点M(4,2)过点M向圆O引切线L求直线L的方程求以M为圆心,且被直线y 2020-07-26 …
设抛物线C:y2=2px(p>0)的焦点为F,准线为l,M∈C,以M为圆心的圆M与l,相切于点Q, 2020-07-26 …
已知点M在椭圆x^2/a^2+y^2/b^2=1(a>b>0)上,以M为圆心的圆与x轴相已知点M在 2020-07-31 …
已知圆O:x2+y2=1和点M(1,4).(1)过点M向圆O引切线,求切线的方程;(2)求以点M为 2020-07-31 …
已知M为圆内弦PQ的中点,过点M作弦AB和CD,连结AD与BC,分别交PQ与点X和Y,并连结AC与 2020-08-01 …