早教吧作业答案频道 -->数学-->
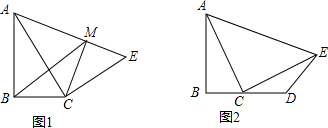
已知△ABC是直角三角形,∠ABC=90°,在△ABC外作直角三角形ACE,∠ACE=90°(1)如图1,过点C作CM⊥AE,垂足为M,连结BM,若AB=AM,求证:BM∥CE;(2)如图2,延长BC至D,使得CD=BC,连结DE,若AB=BD
题目详情
已知△ABC是直角三角形,∠ABC=90°,在△ABC外作直角三角形ACE,∠ACE=90°
(1)如图1,过点C作CM⊥AE,垂足为M,连结BM,若AB=AM,求证:BM∥CE;
(2)如图2,延长BC至D,使得CD=BC,连结DE,若AB=BD,∠EAC=45°,AE=
,求四边形ABDE的面积.
(1)如图1,过点C作CM⊥AE,垂足为M,连结BM,若AB=AM,求证:BM∥CE;
(2)如图2,延长BC至D,使得CD=BC,连结DE,若AB=BD,∠EAC=45°,AE=
| 10 |

▼优质解答
答案和解析
(1)证明:如图1中,
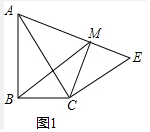
∵CM⊥AE,
∴∠ABC=∠AMC=90°,
在Rt△ACB和Rt△ACM中,
,
∴Rt△ACB≌Rt△ACM,
∴BC=CM,∵AB=AM,
∴BM⊥AC,
∵∠ACE=90°,
∴AC⊥CE,
∴BM∥CE.
(2) 如图2中,作EF⊥BD于F.
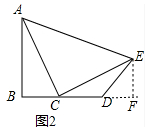
∵∠ACE=90°,∠EAC=45°,
∴∠CAE=∠CEA=45°,
∴CA=CE,∵AE=
,
∴AC=CE=
,
在Rt△ABC中,∵AB=2BC,
∴BC2+4BC2=5,
∴BC=1,AB=2,
∴CB=CD=1,
∵∠ACB+∠BAC=90°,∠ACB+∠ECF=90°,
∴∠BAC=∠ECF,
在△ABC和△CFE中,
,
∴△ABC≌△CFE,
∴BC=EF=1,
∴S四边形ABDE=S△ABC+S△ACE+S△CDE=
×1×2+
×
×
+
×1×1=4.

∵CM⊥AE,
∴∠ABC=∠AMC=90°,
在Rt△ACB和Rt△ACM中,
|
∴Rt△ACB≌Rt△ACM,
∴BC=CM,∵AB=AM,
∴BM⊥AC,
∵∠ACE=90°,
∴AC⊥CE,
∴BM∥CE.
(2) 如图2中,作EF⊥BD于F.

∵∠ACE=90°,∠EAC=45°,
∴∠CAE=∠CEA=45°,
∴CA=CE,∵AE=
| 10 |
∴AC=CE=
| 5 |
在Rt△ABC中,∵AB=2BC,
∴BC2+4BC2=5,
∴BC=1,AB=2,
∴CB=CD=1,
∵∠ACB+∠BAC=90°,∠ACB+∠ECF=90°,
∴∠BAC=∠ECF,
在△ABC和△CFE中,
|
∴△ABC≌△CFE,
∴BC=EF=1,
∴S四边形ABDE=S△ABC+S△ACE+S△CDE=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
| 1 |
| 2 |
看了 已知△ABC是直角三角形,∠...的网友还看了以下:
在五边形ABCD中,∠A=∠D=90,∠B:∠C:∠E=2:3:4,求∠B,∠C,∠E的度数在五边 2020-05-13 …
设有关系模式R(A,B,C,D,E,F) ,其函数依赖集为F={E→D,C→B,CE→F,B→A}。 2020-05-23 …
设有关系模式R(A,B,C,D,E,F),其函数依赖集为F={E→D,C→B,CE→F,B→A}。则 2020-05-24 …
如图,若AB∥CD,则∠B、∠C、∠E三者之间的关系是()A.∠B+∠C+∠E=180°B.∠B+ 2020-06-12 …
你能辨别下列各组字,并用这个字组成一个成语吗?(1)A.戍B.戌C.戎E.戒A.B.C.E.(2) 2020-06-26 …
这5道题用波兰式表达(1)A*(B-C)+T/(D+E)-F/(S*H)(2)A/(B*C(E+F 2020-07-08 …
#include"stdio.h"main(){inta,b,c,e;printf(“please 2020-07-23 …
正方形的6个面分别写着A、B、C、D、E、F,与B、C、E相对的分别是哪个面?F在上面图一上F,前 2020-07-31 …
求解多元一次不等式的编程47a-b-c-d-e-f-g>047b-a-c-d-e-f-g>023c- 2020-12-14 …
C语言运算6、若有代数式,则不正确的C语言表达式是(C).A.a/b/c*e*3B.3*a*e/b/ 2020-12-23 …