如图，已知AD为△ABC的高线，AD=BC，以AB为底边作等腰Rt△ABE，连接ED，EC，延长CE交AD于F点，下列结论：①△ADE≌△BCE；②CE⊥DE；③BD=AF；④S△BDE=S△ACE，其中正确的有（）A.①③B.①②

Question

如图，已知AD为△ABC的高线，AD=BC，以AB为底边作等腰Rt△ABE，连接ED，EC，延长CE交AD于F点，下列结论：①△ADE≌△BCE；②CE⊥DE；③BD=AF；④S_△BDE=S_△ACE，其中正确的有（　　）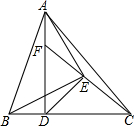

A. ①③

B. ①②④

C. ①②③④

D. ①③④

Answer 1

①∵AD为△ABC的高线，
∴∠CBE+∠ABE+∠BAD=90°，
∵Rt△ABE是等腰直角三角形，
∴∠ABE=∠BAE=∠BAD+∠DAE=45°，AE=BE，
∴∠CBE+∠BAD=45°，
∴∠DAE=∠CBE，
在△DAE和△CBE中，

AE=BE

∠DAE=∠CBE

AD=BC

，
∴△ADE≌△BCE（SAS）；
故①正确；
②∵△ADE≌△BCE，
∴∠EDA=∠ECB，
∵∠ADE+∠EDC=90°，
∴∠EDC+∠ECB=90°，
∴∠DEC=90°，
∴CE⊥DE；
故②正确；
③∵∠BDE=∠ADB+∠ADE，∠AFE=∠ADC+∠ECD，
∴∠BDE=∠AFE，
∵∠BED+∠BEF=∠AEF+∠BEF=90°，
∴∠BED=∠AEF，
在△AEF和△BED中，

∠BDE=∠AFE

∠BED=∠AEF

AE=BE

，
∴△AEF≌△BED（AAS），
∴BD=AF；
故③正确；
④∵AD=BC，BD=AF，
∴CD=DF，
∵AD⊥BC，
∴△FDC是等腰直角三角形，
∵DE⊥CE，
∴EF=CE，
∴S_△AEF=S_△ACE，
∵△AEF≌△BED，
∴S_△AEF=S_△BED，
∴S_△BDE=S_△ACE．
故④正确；
故选C．