早教吧作业答案频道 -->数学-->
在数学探究课上,老师出示了这样的探究问题,请你一起来探究:已知:C是线段AB所在平面内任意一点,分别以AC、BC为边,在AB同侧作等边三角形ACE和BCD,联结AD、BE交于点P.(1)如图1,当
题目详情
在数学探究课上,老师出示了这样的探究问题,请你一起来探究:
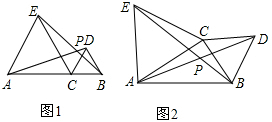
已知:C是线段AB所在平面内任意一点,分别以AC、BC为边,在AB同侧作等边三角形ACE和BCD,联结AD、BE交于点P.
(1)如图1,当点C在线段AB上移动时,线段AD与BE的数量关系是:___.
(2)如图2,当点C在直线AB外,且∠ACB<120°,上面的结论是否还成立?若成立请证明,不成立说明理由.
(3)在(2)的条件下,∠APE的大小是否随着∠ACB的大小的变化而发生变化,若变化,写出变化规律,若不变,请求出∠APE的度数.

已知:C是线段AB所在平面内任意一点,分别以AC、BC为边,在AB同侧作等边三角形ACE和BCD,联结AD、BE交于点P.
(1)如图1,当点C在线段AB上移动时,线段AD与BE的数量关系是:___.
(2)如图2,当点C在直线AB外,且∠ACB<120°,上面的结论是否还成立?若成立请证明,不成立说明理由.
(3)在(2)的条件下,∠APE的大小是否随着∠ACB的大小的变化而发生变化,若变化,写出变化规律,若不变,请求出∠APE的度数.
▼优质解答
答案和解析
(1)∵△ACE、△CBD均为等边三角形,
∴AC=EC,CD=CB,∠ACE=∠BCD,
∴∠ACD=∠ECB;
在△ACD与△ECB中,
,
∴△ACD≌△ECB(SAS),
∴AD=BE,
故答案为AD=BE.
(2)AD=BE成立.
证明:∵△ACE和△BCD是等边三角形
∴EC=AC,BC=DC,
∠ACE=∠BCD=60°,
∴∠ACE+∠ACB=∠BCD+∠ACB,即∠ECB=∠ACD;
在△ECB和△ACD中,
,
∴△ECB≌△ACD(SAS),
∴BE=AD.
(3))∠APE不随着∠ACB的大小发生变化,始终是60°.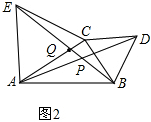
如图2,设BE与AC交于Q,
由(2)可知△ECB≌△ACD,
∴∠BEC=∠DAC
又∵∠AQP=∠EQC,∠AQP+∠QAP+∠APQ=∠EQC+∠CEQ+∠ECQ=180°
∴∠APQ=∠ECQ=60°,即∠APE=60°.
∴AC=EC,CD=CB,∠ACE=∠BCD,
∴∠ACD=∠ECB;
在△ACD与△ECB中,
|
∴△ACD≌△ECB(SAS),
∴AD=BE,
故答案为AD=BE.
(2)AD=BE成立.
证明:∵△ACE和△BCD是等边三角形
∴EC=AC,BC=DC,
∠ACE=∠BCD=60°,
∴∠ACE+∠ACB=∠BCD+∠ACB,即∠ECB=∠ACD;
在△ECB和△ACD中,
|
∴△ECB≌△ACD(SAS),
∴BE=AD.
(3))∠APE不随着∠ACB的大小发生变化,始终是60°.

如图2,设BE与AC交于Q,
由(2)可知△ECB≌△ACD,
∴∠BEC=∠DAC
又∵∠AQP=∠EQC,∠AQP+∠QAP+∠APQ=∠EQC+∠CEQ+∠ECQ=180°
∴∠APQ=∠ECQ=60°,即∠APE=60°.
看了 在数学探究课上,老师出示了这...的网友还看了以下:
如图,抛物线y=ax的平方+bx+c的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.( 2020-05-16 …
下列能体现师生民主平等的情景是()A.数学课上老师误以为小强在自由讲话而批评他,小强大声辩解B.小 2020-05-17 …
已知某容器中发生反应C+H2O(g)=CO+H2已达到平衡状态,加入一定量H2O达到新平衡后C(H 2020-05-21 …
如图,已知三角形ABC将BC边上一点P(点BC除外)向上移动,使BP平分角B,CP平分角C,探究角 2020-07-21 …
在探究杠杆平衡条件的实验中:(1)小明发现杠杆左端低右端高,要使它在水平位置平衡,应将杠杆右端的平 2020-07-29 …
下列不符合对联要求的一项是A.江山指点春光满目,激扬文字彩笔生花。B.国兴旺家兴旺国家兴旺,老平安少 2020-11-23 …
下列能体现师生民主平等的情景是()A.数学课上老师误以为小强在自由讲话而批评他,小强大声辩解B.小刚 2020-11-28 …
科学考察队在北极考察时,为了探究冰曾层下海水的成分.他们在厚薄均匀的冰层上钻一个深达250m的冰洞, 2020-12-19 …
有一个人出生于古印度,被人世间生老病死的景象打动,潜心探索使人摆脱苦难的道理,几年后终于“彻悟”,创 2020-12-20 …
当你遇到或感到老师不公平对待时,作为学生,你应该:()A.找老师评理,指责老师“偏心眼”B.怀恨在心 2021-01-02 …