早教吧作业答案频道 -->数学-->
如图(1),抛物线y=x2+x-4与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线y=x+b与抛物线交于点B、C.(1)求点A的坐标;(2)当b=0时(如图(2)),△ABE与△ACE的面积大小关系
题目详情
如图(1),抛物线y=x 2 +x-4与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线y=x+b与抛物线交于点B、C.
(1)求点A的坐标;
(2)当b=0时(如图(2)),△ABE与△ACE的面积大小关系如何?当b>-4时,上述关系还成立吗,为什么?
(3)是否存在这样的b,使得△BOC是以BC为斜边的直角三角形?若存在,求出b;若不存在,说明理由.
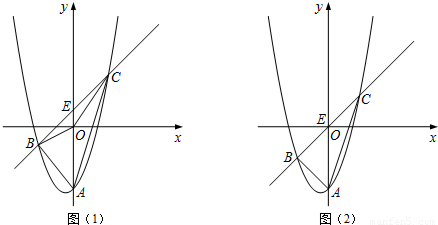
(1)求点A的坐标;
(2)当b=0时(如图(2)),△ABE与△ACE的面积大小关系如何?当b>-4时,上述关系还成立吗,为什么?
(3)是否存在这样的b,使得△BOC是以BC为斜边的直角三角形?若存在,求出b;若不存在,说明理由.

▼优质解答
答案和解析
【答案】分析:(1)知道抛物线的解析式,要求与y轴的交点,令x=0就能求得.(2)当b=0时,直线为y=x,联立两方程式解得交点坐标,由三角形面积公式分别求出两三角形的面积.当b>-4时,仍然联立方程解坐标,作BF⊥y轴,CG⊥y轴,垂足分别为F、G,解得BF和CG的值,再由面积公式求面积值.(3)由BF=CG,∠BEF=∠CEG,∠BFE=∠CGE=90°,可证△BEF≌△CEG,可知BE=CE,即E为BC的中点,当OE=CE时,△OBC为直角三角形,解三角形得到答案.(1)将x=0,代入抛物线解析式,得点A的坐标为(0,-4),(2)当b=0时,直线为y=x,由,解得,.∴B、C的坐标分别为(-2,-2),(2,2),,∴S△ABE=S△ACE.当b>-4时,仍有S△ABE=S△ACE成立.理由如下由,解得,.故B、C的坐标分别为(-,-+b),(,+b),作BF⊥y轴,CG⊥y轴,垂足分别为F、G,则,而△ABE和△ACE是同底的两个三角形,∴S△ABE=S△ACE.(3)存在这样的b,∵BF=CG,∠BEF=∠CEG,∠BFE=∠CGE=90°,∴△BEF≌△CEG,∴BE=CE,即E为BC的中点,∴当OE=CE时,OE=BC,此时△OBC为直角三角形.∵,∴,而OE=|b|,∴,解得b1=4,b2=-2,∴当b=4或-2时,△OBC为直角三角形.点评:本题主要考查二次函数的应用,是一道综合性很强的习题,做题需要细心.
看了 如图(1),抛物线y=x2+...的网友还看了以下:
二次函数.已知抛物线的顶点为P(3,-2),且在X轴上截得的线段AB长为4.1)求抛物线解析式2)抛 2020-03-30 …
如图,抛物线y=-x^2+bx+c经过点A(1,0)和点B(0,5).(1)求此抛物线的解析式及顶 2020-05-16 …
知道抛物线的顶点坐标,如何求抛物线的解析式 2020-05-22 …
斜抛运动中如果抛出点和落地点不在一个水平面上升和下降的时间还相等么如果相等为什么啊从空中抛出如果以 2020-06-20 …
抛物线y=-14(x-1)2+3与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.(1)如图1. 2020-07-26 …
如果已知抛物线与x轴相交的2个点坐标,如何求抛物线解析式?如题如题 2020-07-26 …
已知抛物线m的顶点为M,抛物线m上部分点的横坐标与对应的纵坐标如下表:x…-2023…y…5-3- 2020-08-02 …
经过两点(1,0)(3,0),且顶点为M的抛物线```急啊经过两点(1,0)(3,0),且顶点为M的 2020-11-24 …
如图,一小球从斜坡O点抛出,球的抛出路线可以用二次函数y=-x2+4x刻画,斜坡可以用一次函数y=1 2020-12-09 …
知道中点坐标直线斜率怎么求我有一道题目抛物线x2=6y的一条弦的中点为M(1,2)求弦所在的直线方程 2021-02-03 …