早教吧作业答案频道 -->数学-->
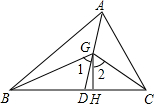
如图,在△ABC中,AD是它的角平分线,G是AD上的一点,BG,CG分别平分∠ABC,∠ACB,GH⊥BC,垂足为H,求证:(1)∠BGC=90°+12∠BAC;(2)∠1=∠2.
题目详情
如图,在△ABC中,AD是它的角平分线,G是AD上的一点,BG,CG分别平分∠ABC,∠ACB,GH⊥BC,垂足为H,求证:
(1)∠BGC=90°+
∠BAC;
(2)∠1=∠2.

(1)∠BGC=90°+
| 1 |
| 2 |
(2)∠1=∠2.
▼优质解答
答案和解析
(1)由三角形内角和定理可知:∠ABC+∠ACB=180°-∠BAC,
∵BG,CG分别平分∠ABC,∠ACB,
∠GBC=
∠ABC,∠GCB=
∠ACB
∴∠GBC+∠GCB=
(∠ABC+∠ACB)=
(180°-∠BAC)=90°-
∠BAC
∴∠BGC=180°-(∠GBC+∠GCB)=180°-
(∠ABC+∠ACB)=90°+
∠BAC;
(2)∵AD是它的角平分线,
∴∠BAD=∠CAD
∴∠1=∠BAD+∠ABG,
∵GH⊥BC,
∴∠GHC=90°
∴∠2=90°-∠GCH
=90°-
∠ACB
=90°-
(180°-∠DAC-∠ADC)
=
∠DAC+
∠ADC
∵∠ADC=∠ABC+∠BAD,
∴
∠ADC=
∠ABC+∠
∠BAD
=∠ABG+
∠BAD,
∴∠2=
∠DAC+
∠ADC
=
∠BAD+
∠BAD+∠ABG
=∠BAD+∠ABG,
∴∠1=∠2,
∵BG,CG分别平分∠ABC,∠ACB,
∠GBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠GBC+∠GCB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BGC=180°-(∠GBC+∠GCB)=180°-
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵AD是它的角平分线,
∴∠BAD=∠CAD
∴∠1=∠BAD+∠ABG,
∵GH⊥BC,
∴∠GHC=90°
∴∠2=90°-∠GCH
=90°-
| 1 |
| 2 |
=90°-
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ADC=∠ABC+∠BAD,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=∠ABG+
| 1 |
| 2 |
∴∠2=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=∠BAD+∠ABG,
∴∠1=∠2,
看了 如图,在△ABC中,AD是它...的网友还看了以下:
A市在B市的12km的位置,给B市发货的车以40km/时送货,以60km/时返回A市,往返1时10 2020-04-27 …
有机物A~H间存在如下的转化关系:已知:①F的结构中含有一个苯环,且仅含两个邻位的取代基;②H的结 2020-05-02 …
杂化轨道理论问题拿Nh3做例子吧,明明N原子2P轨道有3个未成对电子,可以达到结合3个H原子的条件 2020-05-13 …
pH相同的盐酸和醋酸两种溶液中,它们的()A.H+的物质的量相同B.物质的量浓度相同C.H+的物质 2020-05-15 …
点燃一支长20cm蜡烛,其燃烧时剩下的高度h(cm)与燃烧的时间t(h)的函数关系(1)这支蜡烛可 2020-05-16 …
蜡烛燃烧时,剩下的长度h(cm)是燃烧时间t(h)的一次函数,现测得蜡烛燃烧1h后,其长度为15c 2020-05-16 …
一列质量为1000t的火车,以180km/h的速度在平直轨道上匀速行驶,整列火车收到的阻力是全力的 2020-05-16 …
一列货车以28.8km/h的速度在平直铁路上行驶,由于调度事故,在后方700m处有一列快车以72k 2020-05-16 …
小明骑自行车从家去小周家,先以12km/h的速度走过一段平路,到小周家共用55min,回来时,他用 2020-05-23 …
co2与H+和OH-的反应为什么CO2是先和溶液中的H+反应,而当CO2过量时才与OH-反应?与O 2020-05-24 …