早教吧作业答案频道 -->数学-->
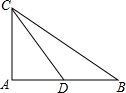
如图,在△ABC中,∠CAB=90°,AB=6,AC=4,CD是△ABC的中线,将△ABC沿直线CD翻折,点B′是点B的对应点,点E是线段CD上的点,如果∠CAE=∠BAB′,那么CE的长是.
题目详情
如图,在△ABC中,∠CAB=90°,AB=6,AC=4,CD是△ABC的中线,将△ABC沿直线CD翻折,点B′是点B的对应点,点E是线段CD上的点,如果∠CAE=∠BAB′,那么CE的长是___.

▼优质解答
答案和解析
如图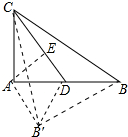 ,∵△CDB′是由□CDB翻折,
,∵△CDB′是由□CDB翻折,
∴∠BCD=∠DCB′,∠CBD=∠CDB′,AD=DB=DB′,
∴∠DBB′=∠DB′B,
∵2∠DCB+2∠CBD+2∠DBB′=180°,
∴∠DCB+∠CBD+∠DBB′=90°,
∵∠CDA=∠CDB+∠CBD,∠ACD+∠CDA=180°,
∴∠ABB′=∠ACE,
∵AD=DB=DB′=3,
∴∠AB′B=90°,
∵∠ACE=∠ABB′,∠CAE=∠BAB′,
∴△ACE∽△ABB′,
∴∠AEC=∠AB′B=90°,
在RT△AEC中,∵AC=4,AD=3,
∴CD=
=5,
∵
AC•AD=
•CD•AE,
∴AE=
=
,
在RT△ACE中,CE=
=
=
.
故答案为
.
 ,∵△CDB′是由□CDB翻折,
,∵△CDB′是由□CDB翻折,∴∠BCD=∠DCB′,∠CBD=∠CDB′,AD=DB=DB′,
∴∠DBB′=∠DB′B,
∵2∠DCB+2∠CBD+2∠DBB′=180°,
∴∠DCB+∠CBD+∠DBB′=90°,
∵∠CDA=∠CDB+∠CBD,∠ACD+∠CDA=180°,
∴∠ABB′=∠ACE,
∵AD=DB=DB′=3,
∴∠AB′B=90°,
∵∠ACE=∠ABB′,∠CAE=∠BAB′,
∴△ACE∽△ABB′,
∴∠AEC=∠AB′B=90°,
在RT△AEC中,∵AC=4,AD=3,
∴CD=
| AC2+AD2 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴AE=
| AC•AD |
| CD |
| 12 |
| 5 |
在RT△ACE中,CE=
| AC2-AE2 |
42-(
|
| 16 |
| 5 |
故答案为
| 16 |
| 5 |
看了 如图,在△ABC中,∠CAB...的网友还看了以下:
1已知点A在Y轴正半轴上且与点P(4,4)的距离等于5则点A的坐标为多少 2 已知点F在X轴上且与 2020-04-06 …
1.平面直角坐标系内点A(n,1-n)一定不在A:第1象限B第2象限C:第3象限D:第4象限2.已 2020-05-14 …
y=根号(x^2+4)-根号(x^2+2x+10)就是点P(x,0)到点A(0,-4)和点B(-1 2020-06-03 …
一个求4个支点的力学题一个长方体4*4*1m吧.有4个支点在4个角上,它的重心偏移了长1m,宽0. 2020-06-03 …
OTDR测量故障点时,A点到B点测量光纤事件表显示(4芯)其中3芯显示0.2KM,一芯显示0.28 2020-06-07 …
3点28分的英文1.3点282.4点093.12点454.8点395.1点586.4点107.5点 2020-06-11 …
如果一个小正方形的对角线长10m,则点(0,0)东偏北45°方向30m处是点(,);点(4,2)南 2020-06-12 …
规定,点P(a,b)为方程ax=b的“特征点”.如:方程3x=-4的“特征点”是(3,-4),方程 2020-06-19 …
有一挂钟,几点钟就敲响几下,半点敲响一下,那么从1点到4点(含1点和4点)共敲响几下?为什么是1+ 2020-06-23 …
1.已知A(1,2),B(3,4)直线L1:x=0L2:y=0和L3:x+3y-1=0.设Pi是L 2020-07-14 …