已知函数f（x）=-x，x≤0-x2+2x，x>0，若方程f2（x）+bf（x）+14=0有六个相异实根，则实数b的取值范围（）A.（-2，0）B.（-2，-1）C.（-54，0）D.（-54，-1）

Question

已知函数f（x）=

-x，x≤0

-x2+2x，x>0

，若方程f²（x）+bf（x）+(1)/(4)=0有六个相异实根，则实数b的取值范围（　　）

A. （-2，0）

B. （-2，-1）

C. （-

(5)/(4)，0）

D. （-

(5)/(4)，-1）

Answer 1

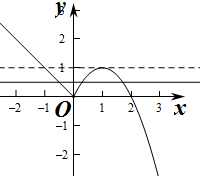令t=f（x），则原函数方程等价为t²+bt+(1)/(4)=0．
作出函数f（x）的图象如图：
图象可知当由0<t<1时，函数t=f（x）有3个交点．
所以要使f²（x）+bf（x）+(1)/(4)=0有六个相异实根，
则等价为有两个根t₁，t₂，
且0<t₁<1，0<t₂<1．
令g（t）=t²+bt+(1)/(4)，
则由根的分布（如下图）可得

△>0

f(0)=(1)/(4)>0

f(1)=1+b+(1)/(4)>0

0<-(b)/(2)<1

，即

b2-1>0

b>-(5)/(4)

-2<b<0

，即

b>1或b<-1

b>-(5)/(4)

-2<b<0

，
解得-(5)/(4)<b<-1，
则实数b的取值范围是（-(5)/(4)，-1）．

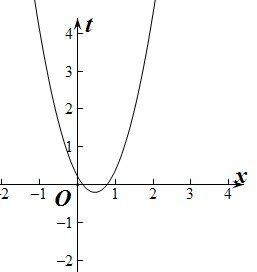
故选：D．