早教吧作业答案频道 -->数学-->
已知定义在R上的函数f(x)满足f(log2x)=x+(a为常数).(1)求f(x)的解析式;(2)当f(x)是偶函数时,试讨论f(x)的单调性.
题目详情
已知定义在R上的函数f(x)满足f(log 2 x)=x+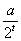 (a为常数).
(a为常数).
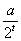 (a为常数).
(a为常数).
(1)求f(x)的解析式;
(2)当f(x)是偶函数时,试讨论f(x)的单调性.
▼优质解答
答案和解析
解析:
(1)设log2x=t 则x=2t ∴f(t)=2t+ ∴f(x)=2x+(x∈R).(2)若f(x)是偶函数,则f(-x)=f(x) 即 即 ∴(2x-2-x)(a-1)=0对x∈R恒成立,∴a=1.∴f(x)=2x+(x∈R).设x1<x2 则f(x1)-f(x2)=∵x1<x2 ∴>0.①若x1 x2∈(-∞ 0] 则x1+x2<0 ∴<1.∴f(x1)-f(x2)>0 f(x1)>f(x2).故函数f(x)在(-∞,0]上是减函数.②当x1、x2∈(0 +∞) 则x1+x2>0 ∴>1.∴f(x1)-f(x2)<0即f(x1)<f(x2).故函数f(x)在(0 +∞)上是增函数.或由f(x)是偶函数且在(-∞,0]上是减函数 由对称性可知f(x)在(0 +∞)上是增函数.
解析:
(1)设log2x=t 则x=2t ∴f(t)=2t+ ∴f(x)=2x+(x∈R).(2)若f(x)是偶函数,则f(-x)=f(x) 即 即 ∴(2x-2-x)(a-1)=0对x∈R恒成立,∴a=1.∴f(x)=2x+(x∈R).设x1<x2 则f(x1)-f(x2)=∵x1<x2 ∴>0.①若x1 x2∈(-∞ 0] 则x1+x2<0 ∴<1.∴f(x1)-f(x2)>0 f(x1)>f(x2).故函数f(x)在(-∞,0]上是减函数.②当x1、x2∈(0 +∞) 则x1+x2>0 ∴>1.∴f(x1)-f(x2)<0即f(x1)<f(x2).故函数f(x)在(0 +∞)上是增函数.或由f(x)是偶函数且在(-∞,0]上是减函数 由对称性可知f(x)在(0 +∞)上是增函数.
看了 已知定义在R上的函数f(x)...的网友还看了以下:
已知函数f(x)=a-1/绝对值x a∈r 1若函数f(x)的定义域和值域为[1/2,2].求实数 2020-05-16 …
已知函数f(x)=logax+b/x-b(a>0,b>0,a≠1) 《1》求f(x)的定义域 《2 2020-05-16 …
1,若函数y=f(x)的定义域为[3,8]试求f(x^2-8x+15)的定义域1,若函数y=f(x 2020-05-20 …
若函数f(x)的定义域为0,1,求g(x)=f(x+m)+f(x-m)(m>0)的定义域中的讨论当 2020-06-22 …
试构造函数f(x),g(x),其定义域为(0,1),值域为[0,1]并满足如下条件:试构造函数f( 2020-07-26 …
已知函数f1(x)=3|x−p1|,f2(x)=2•3|x−p2|(p1,p2为实数),函数f(x) 2020-12-23 …
问了很多人都不懂已知集合A={X丨X=m+1/6,m属于Z},B={X丨X=n/2-1/3,n属于Z 2021-01-12 …
若关于x的方程2k/(x-1)-x/(x^2-x)=(kx+1)/x只有一个解,试探讨k的取值并求出 2021-01-12 …
试探讨方程ax=b的解的情况.当a不等于o时,方程有唯解x=b除以a,当a=o=b时,方程试探讨方程 2021-01-12 …
已知函数F=(x)=x+1/x-1,(1)求F(x)的定义域和值域已知函数F=(x)=x+1/x-1 2021-01-31 …