早教吧作业答案频道 -->数学-->
如图,抛物线y=ax2+3x+c经过A(-1,0),B(4,0)两点,与y轴交于点C.(1)求抛物线的解析式;(2)若点P在第一象限的抛物线上,且点P的横坐标为t,过点P向x轴作垂线交直线BC于点Q,设线
题目详情
如图,抛物线y=ax2+3x+c经过A(-1,0),B(4,0)两点,与y轴交于点C.
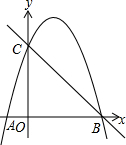
(1)求抛物线的解析式;
(2)若点P在第一象限的抛物线上,且点P的横坐标为t,过点P向x轴作垂线交直线BC于点Q,设线段PQ的长为m,求m与t之间的函数关系式,并求出m的最大值;
(3)在(2)的条件下,抛物线上点D(不与C重合)的纵坐标为m的最大值,在x轴上找一点E,使点B、C、D、E为顶点的四边形是平行四边形,请直接写出E点坐标.

(1)求抛物线的解析式;
(2)若点P在第一象限的抛物线上,且点P的横坐标为t,过点P向x轴作垂线交直线BC于点Q,设线段PQ的长为m,求m与t之间的函数关系式,并求出m的最大值;
(3)在(2)的条件下,抛物线上点D(不与C重合)的纵坐标为m的最大值,在x轴上找一点E,使点B、C、D、E为顶点的四边形是平行四边形,请直接写出E点坐标.
▼优质解答
答案和解析
解(1)∵抛物线y=ax2+3x+c经过A(-1,0),B(4,0)两点,
∴
.
解得:a=-1,c=4.
∴抛物线的解析式为y=-x2+3x+4.
(2)∵将x=0代入抛物线的解析式得:y=4,
∴C(0,4).
设直线BC的解析式为y=kx+b.
∵将B(4,0),C(0,4)代入得:
,解得:k=-1,b=4
∴直线BC的解析式为:y=-x+4.
过点P作x的垂线PQ,如图所示:
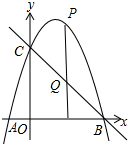
∵点P的横坐标为t,
∴P(t,-t2+3t+4),Q(t,-t+4).
∴PQ=-t2+3t+4-(-t+4)=-t2+4t.
∴m=-t2+4t=-(t-2)2+4(0<t<4).
∴当t=2时,m的最大值为4.
(3)将y=4代入抛物线的解析式得:-x2+3x+4=4.
解得:x1=0,x2=3.
∵点D与点C不重合,
∴点D的坐标为(3,4).
又∵C(0,4)
∴CD∥x轴,CD=3.
∴当BE=CD=3时,B、C、D、E为顶点的四边形是平行四边形.
∴点E(1,0)或(7,0).
∴
|
解得:a=-1,c=4.
∴抛物线的解析式为y=-x2+3x+4.
(2)∵将x=0代入抛物线的解析式得:y=4,
∴C(0,4).
设直线BC的解析式为y=kx+b.
∵将B(4,0),C(0,4)代入得:
|
∴直线BC的解析式为:y=-x+4.
过点P作x的垂线PQ,如图所示:

∵点P的横坐标为t,
∴P(t,-t2+3t+4),Q(t,-t+4).
∴PQ=-t2+3t+4-(-t+4)=-t2+4t.
∴m=-t2+4t=-(t-2)2+4(0<t<4).
∴当t=2时,m的最大值为4.
(3)将y=4代入抛物线的解析式得:-x2+3x+4=4.
解得:x1=0,x2=3.
∵点D与点C不重合,
∴点D的坐标为(3,4).
又∵C(0,4)
∴CD∥x轴,CD=3.
∴当BE=CD=3时,B、C、D、E为顶点的四边形是平行四边形.
∴点E(1,0)或(7,0).
看了 如图,抛物线y=ax2+3x...的网友还看了以下:
马上交~改为一般疑问句,做肯定否定回答,并改为否定句Wearegoodfriends?Theyha 2020-05-23 …
修改病句(只有两句有毛病)1.我店刚到鲁迅的小说集和2.分别有精装和简装两种版本3.精装本封面,插 2020-06-06 …
参数方程极坐标直线截曲线,P在直线上,交点为A、B,求|PA|*|PB|已知t1t2,那就是求t1 2020-06-27 …
角AOB的边上有3个点,边OB上有4个点,以OA边上一个点和OB边上一个点为端点做线段,线段交点最 2020-07-09 …
如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴交 2020-07-13 …
已知抛物线C:x2=2py(p>0)的焦点为F,直线x=4与x轴的交点为P,与C的交点为Q,且|Q 2020-07-20 …
求一个大智慧公式,成交量为前一日2倍以上,涨幅小于5%,振幅大于4%成交量为前一日2倍以上,涨幅小 2020-07-23 …
如图,二次函数y=-x2+3x+m的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相 2020-07-31 …
已知:A.B是圆x2+y2=4与x轴的两个交点,P为直线l:x=4上的动点,PA.PB与圆x^2+ 2020-07-31 …
在三角形ABC中,D是BC上靠近C的三等分点,E是AD中点,已知三角形ABC的面积是1.连接BE的延 2020-11-28 …