早教吧作业答案频道 -->数学-->
已知:平行四边形ABCD在直角坐标系中的位置如图,O是坐标原点,OB:OC:OA=1:3:5,S□ABCD=12,抛物线经过D、A、B三点.①求A、C两点的坐标;②求抛物线解析式;③E是抛物线与DC交点,以DE
题目详情
已知:平行四边形ABCD在直角坐标系中的位置如图,O是坐标原点,OB:OC:OA=1:3:5,S□ABCD=12,抛物线经过D、A、B三点.
①求A、C两点的坐标;
②求抛物线解析式;
③E是抛物线与DC交点,以DE为边的平行四边形,它的面积与ABCD面积相等,且另两顶点为P、N中有一个顶点P在抛物线上.求P点和N点的坐标.
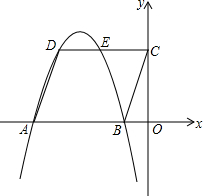
①求A、C两点的坐标;
②求抛物线解析式;
③E是抛物线与DC交点,以DE为边的平行四边形,它的面积与ABCD面积相等,且另两顶点为P、N中有一个顶点P在抛物线上.求P点和N点的坐标.

▼优质解答
答案和解析
(1)∵OB:OC:OA=1:3:5,
设OB=x,OC=3x,OA=5x,
∴AB=OA-OB=5x-x=4x,
∵S▱ABCD=12,
∴AB•OC=4x×3x=12,解得x=1,
∴OB=1,OC=3,OA=5,
∴A(-5,0),C(0,3),
(2)∵OB=1,OC=3,OA=5,
∴AB=4,
∵四边形ABCD是平行四边形,
∴AB=CD=4,
∴D(-4,3),
∵A(-5,0),B(-1,0),
设抛物线的解析式为y=ax2+bx+c,
∴
,解得
,
∴抛物线的解析式为y=-x2-6x-5.
(3)∵E点的纵坐标为3,
∴-x2-6x-5=3.解得x=-2或x=-4,
∴E的坐标为(-2,3),
∴DE=-2-(-4)=2,
∴以DE为边的平行四边形的面积与▱ABCD面积相等,
∴P点到直线DE的距离为,12÷2=6,
∴P的纵坐标为-3,
把y=-3代入y=-x2-6x-5得-x2-6x-5=-3,解得,x=-3+
或x=-3-
,
∴P的坐标为(-3+
,-3)或(-3-
,-3).
设OB=x,OC=3x,OA=5x,
∴AB=OA-OB=5x-x=4x,
∵S▱ABCD=12,
∴AB•OC=4x×3x=12,解得x=1,
∴OB=1,OC=3,OA=5,
∴A(-5,0),C(0,3),
(2)∵OB=1,OC=3,OA=5,
∴AB=4,
∵四边形ABCD是平行四边形,
∴AB=CD=4,
∴D(-4,3),
∵A(-5,0),B(-1,0),
设抛物线的解析式为y=ax2+bx+c,
∴
|
|
∴抛物线的解析式为y=-x2-6x-5.
(3)∵E点的纵坐标为3,
∴-x2-6x-5=3.解得x=-2或x=-4,
∴E的坐标为(-2,3),
∴DE=-2-(-4)=2,
∴以DE为边的平行四边形的面积与▱ABCD面积相等,
∴P点到直线DE的距离为,12÷2=6,
∴P的纵坐标为-3,
把y=-3代入y=-x2-6x-5得-x2-6x-5=-3,解得,x=-3+
| 7 |
| 7 |
∴P的坐标为(-3+
| 7 |
| 7 |
看了 已知:平行四边形ABCD在直...的网友还看了以下:
若a+b=b+c,则a-b(c为整式)若a=b,则ac=bc(c为整式)若ac=bc,则a=b(c 2020-04-22 …
由a=b一定可以得出的等式是()A.a÷c=b÷c由a=b一定可以得出的等式是()A.a÷c=b÷ 2020-06-06 …
在三角形ABC中,如果AB边上的高与AB边的长相等,则AC/BC+BC/AC+AB^2/BC*AC 2020-07-22 …
如图为一梯级平面图,一只老鼠沿长方形的两边A-B-C的路线逃跑,一只猫同时沿梯级(折线)A-C-D 2020-07-25 …
下图为一梯级平面图,一只老鼠沿长方形的两边A-B-C的路线逃跑,一只猫同时沿梯级(折线)A-C-D 2020-07-25 …
三角形的三条边分别是a,b,c,若满足a+b=2c,那么这个三角形是什么三角形?三角形的三条边分别 2020-08-03 …
100%收购公司其中一名法人股东涉及到的问题事实:A.B.C.D为四个法人。A.B公司为C公司的股东 2020-11-06 …
如图三条曲线表示C、Si和P元素的四级电离能变化趋势.下列说法正确的是()A.电负性:c>b>aB. 2020-11-11 …
在三角形ABC和三角形A'B'C'中CD,C'D'分别是高,并且AC=A'C;,CD=C'D',∠A 2020-11-28 …
已知三角形ABC的内角A,B,C所对的边分别为a,b,c,.已知三角形ABC的内角A,B,C所对的边 2021-02-07 …