早教吧作业答案频道 -->数学-->
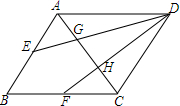
如图，在△ABC中，E，F分别为AB，BC边上的中点，G，H是AC的三等分点，EG，FH的延长线交于点D．求证：①DG：EG=2：1；②四边形ABCD是平行四边形．
题目详情
如图，在△ABC中，E，F分别为AB，BC边上的中点，G，H是AC的三等分点，EG，FH的延长线交于点D．求证：①DG：EG=2：1；②四边形ABCD是平行四边形．
▼优质解答
答案和解析
证明：②连接BD交AC于O，连结BG，BH，如图所示：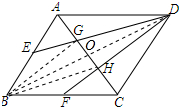
∵E是AB中点，AG=GH
∴AE=BE，EG是△ABH的一条中位线，
∴EG∥BH，即GD∥BH，
同理可证BG∥DH，
∴四边形BHDG是平行四边形．
∴BO=OD，GO=OH，
又∵AG=HC，
∴AG+GO=HC+OH，
即AO=OC，
又∵BO=OD，
∴四边形ABCD是平行四边形；
①∵四边形ABCD是平行四边形，
∴AB=CD=2AE，AB∥CD，
∴△CDG∽△AEG，
∴DG：EG=CD：AE=2：1．
∵E是AB中点，AG=GH
∴AE=BE，EG是△ABH的一条中位线，
∴EG∥BH，即GD∥BH，
同理可证BG∥DH，
∴四边形BHDG是平行四边形．
∴BO=OD，GO=OH，
又∵AG=HC，
∴AG+GO=HC+OH，
即AO=OC，
又∵BO=OD，
∴四边形ABCD是平行四边形；
①∵四边形ABCD是平行四边形，
∴AB=CD=2AE，AB∥CD，
∴△CDG∽△AEG，
∴DG：EG=CD：AE=2：1．
看了 如图，在△ABC中，E，F分...的网友还看了以下：
正方形ABCD的边CD在正方形ECGF的边CE上,B.C.G三点在一条直线上,切边常为4和6若点m 2020-04-27 …
如图,正方形ABCD的边长为1,G是CD边上的一个动点(G不与C、D重合),以CG为一边向正方如图 2020-05-16 …
在棱长为一的正方体ABCD-A,B,C,D,中,E是BD的中点,G在棱CD上且CG=1/4DC,F 2020-05-16 …
在直角坐标系中,E.F分别是X轴负半轴和正半轴上一点,G是Y轴正半轴一点,且∠OGE=∠OGH.（ 2020-06-02 …
3.下列句子中加点词语感情色彩没有发生变化的一项是()A.也有解散辫子……还要将脖子扭几扭。实在标 2020-07-08 …
高等数学：设函数f(x)和g(x)在(-无穷，+无穷)内有定义，f(x)为连续函数，且f(x)≠0 2020-07-21 …
已知椭圆E:x^2/8+y^2/4=1的左焦点为F,左准线l与x轴的交点是圆C的圆心,圆C恰好经过 2020-07-31 …
求解一题证明题!高数设f(x)与g(x)在[a,b]上连续,在(a,b)上可导,f(a)=f(b) 2020-08-01 …
三角形abc三个顶点分别为a（x1,y1）,b（x2,y2）c（x3,y3）,d是边ab的中点,g是 2020-10-31 …
如图,在正方形ABCD中,G是BC上的任意一点（G与B,C两点不重合）,E,F是AG上的两点（E,F 2021-01-11 …