早教吧作业答案频道 -->数学-->
已知二次函数y=ax2+bx+c(a≠0)图象如图,有下列8个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1的实数);⑥2a+b=0;⑦b2-4ac≤0;⑧(a+c)2>b2其中正确的结论
题目详情
已知二次函数y=ax2+bx+c(a≠0)图象如图,有下列8个结论:
①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1的实数);⑥2a+b=0;⑦b2-4ac≤0;⑧(a+c)2>b2
其中正确的结论有___.
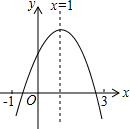
①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1的实数);⑥2a+b=0;⑦b2-4ac≤0;⑧(a+c)2>b2
其中正确的结论有___.
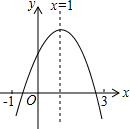
▼优质解答
答案和解析
①由抛物线的开口方向向下可推出a<0,
因为对称轴在y轴右侧,对称轴为x=-
>0,
而a<0,所以b>0,
由抛物线与y轴的交点在y轴的正半轴上,可知c>0,故abc<0,错误;
②当x=-1时,y<0,∴a-b+c<0,a+c<b,错误;
③当x=2时,y>0,∴4a+2b+c>0,正确;
④对称轴为x=-
=1,∴a=-
,∵a-b+c<0,∴-
-b+c<0,∴2c<3b,正确;
⑤∵当x=1时有最大值y=a+b+c,∴a+b+c>am2+bm+c,∴a+b>m(am+b)(m≠1的实数),正确;
⑥对称轴为x=-
=1,∴b=-2a,∴2a+b=0,正确;
⑦抛物线与x轴有两个交点,∴b2-4ac>0,错误;
⑧∵x=1时,y=a+b+c>0,x=-1时,y=a-b+c<0,
∴(a+b+c)(a-b+c)<0,
即[(a+c)+b][(a+c)-b]=(a+c)2-b2<0,
∴(a+c)2<b2,正确..
综上可得:③④⑤⑥⑧正确.
故答案为③④⑤⑥⑧.
因为对称轴在y轴右侧,对称轴为x=-
| b |
| 2a |
而a<0,所以b>0,
由抛物线与y轴的交点在y轴的正半轴上,可知c>0,故abc<0,错误;
②当x=-1时,y<0,∴a-b+c<0,a+c<b,错误;
③当x=2时,y>0,∴4a+2b+c>0,正确;
④对称轴为x=-
| b |
| 2a |
| b |
| 2 |
| b |
| 2 |
⑤∵当x=1时有最大值y=a+b+c,∴a+b+c>am2+bm+c,∴a+b>m(am+b)(m≠1的实数),正确;
⑥对称轴为x=-
| b |
| 2a |
⑦抛物线与x轴有两个交点,∴b2-4ac>0,错误;
⑧∵x=1时,y=a+b+c>0,x=-1时,y=a-b+c<0,
∴(a+b+c)(a-b+c)<0,
即[(a+c)+b][(a+c)-b]=(a+c)2-b2<0,
∴(a+c)2<b2,正确..
综上可得:③④⑤⑥⑧正确.
故答案为③④⑤⑥⑧.
看了 已知二次函数y=ax2+bx...的网友还看了以下:
我想要请问小学数学问题1.108个0.1比9500个0.001大2.254个0.01加上()个0. 2020-04-07 …
一个小数里面有500个0.001,这个小数是(什么).小数点的末尾添上"0"或去掉"0",小数的一 2020-04-11 …
(1)0.62里有()个0.01;1里面有()个0.1;100个((1)0.62里有()个0.01 2020-04-27 …
0.276是由几个0.1,几个0.01和几个0.001组成的.一个小数的计数单位是0.001,他比 2020-05-20 …
1.已知a=0.(20个0)35,b=0.(21个0)1,求a+b2.a=0.(100个0)35, 2020-06-06 …
interfaceEthernet0/0/0和interfaceGigabitEthernet1/ 2020-06-27 …
请问做一套布艺沙发套要用多少布料?尺寸如下:1.83*0.89*0.745.0.14*1个1.04 2020-06-27 …
a=0.00.(10个0)022b=0.00.(12个0)050求a*b=?a=0.00.(10个 2020-07-16 …
车厢的体积是:5.69米X2.13米X2.18米,我要装的货物规格是:0.55*0.315*0.56 2020-11-03 …
2、128个0.01是(),48个是()1/1000.3、7个千,2个十,3个百分之一,5个万分之一 2020-12-17 …