某校高一共录取新生1000名，为了解学生视力情况，校医随机抽取了100名学生进行视力测试，并得到如下频率分布直方图．（Ⅰ）若视力在4.6～4.8的学生有24人，试估计高一新生视力在4.8以上

Question

某校高一共录取新生1000名，为了解学生视力情况，校医随机抽取了100名学生进行视力测试，并得到如下频率分布直方图．

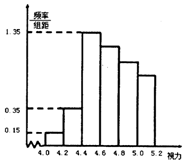
（Ⅰ）若视力在4.6～4.8的学生有24人，试估计高一新生视力在4.8以上的人数；

	1～50名	951～1000名
近视	41	32
不近视	9	18

（Ⅱ）校医发现学习成绩较高的学生近视率较高，又在抽取的100名学生中，对成绩在前50名的学生和其他学生分别进行统计，得到如右数据，根据这些数据，校医能否有超过95%的把握认为近视与学习成绩有关？
（Ⅲ）用分层抽样的方法从（Ⅱ）中27名不近视的学生中抽出6人，再从这6人中任抽2人，其中抽到成绩在前50名的学生人数为ξ，求ξ的分布列和数学期望．
附：K²=(n(ad-bc)2)/((a+b)(c+d)(a+c)(b+d))

P（K2≥k）	0.10	0.05	0.025	0.010	0.005
k	2.706	3.841	5.024	6.635	7.879

Answer 1

（Ⅰ）由图可知，前四组学生的视力在4.8以下，第一组有0.15×0.2×100=3人，第二组有0.35×0.2×100=7人，第三组1.35×0.2×100=27人，第四组有24人．…（2分）
所以视力在4.8以上的人数为1000×(100-3-7-27-24)/(100)=390
人．…（4分）
（Ⅱ）K2=(100×(41×18-32×9)2)/(50×50×73×27)=(300)/(73)≈4.110>3.841
，因此校医有超过95%的把握认为近视与成绩有关．…（8分）
（Ⅲ）依题意，6人中年级名次在1～50名和951～1000名的分别有2人和4人，所以ξ可取0，1，2.P(ξ=0)=(C24)/(C26)=(2)/(5)，P(ξ=1)=(C14C12)/(C26)=(8)/(15)，P(ξ=2)=(C22)/(C26)=(1)/(15)，
ξ的分布列为

ξ	0	1	2
P	(2)/(5)	(8)/(15)	(1)/(15)

…（10分）
ξ的数学期望E(ξ)=0×(2)/(5)+1×(8)/(15)+2×(1)/(15)=(2)/(3)．…（12分）