早教吧作业答案频道 -->数学-->
问题情境如图1,Rt△ABC中,∠ACB=90°,CD⊥AB,我们可以利用△ABC与△ACD相似证明AC2=AD•AB,这个结论我们称之为射影定理,试证明这个定理;结论运用如图2,正方形ABCD的边长为6,
题目详情
【问题情境】如图1,Rt△ABC中,∠ACB=90°,CD⊥AB,我们可以利用△ABC与△ACD相似证明AC2=AD•AB,这个结论我们称之为射影定理,试证明这个定理;
【结论运用】如图2,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,过点C作CF⊥BE,垂足为F,连接OF,
(1)试利用射影定理证明△BOF∽△BED;
(2)若DE=2CE,求OF的长.
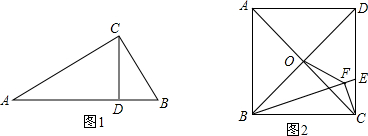
【结论运用】如图2,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,过点C作CF⊥BE,垂足为F,连接OF,
(1)试利用射影定理证明△BOF∽△BED;
(2)若DE=2CE,求OF的长.
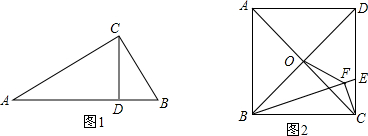
▼优质解答
答案和解析
【问题情境】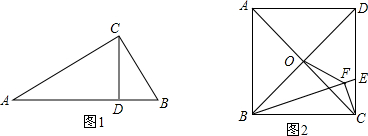
证明:如图1,
∵CD⊥AB,
∴∠ADC=90°,
而∠CAD=∠BAC,
∴Rt△ACD∽Rt△ABC,
∴AC:AB=AD:AC,
∴AC2=AD•AB;
【结论运用】
(1)证明:如图2,
∵四边形ABCD为正方形,
∴OC⊥BO,∠BCD=90°,
∴BC2=BO•BD,
∵CF⊥BE,
∴BC2=BF•BE,
∴BO•BD=BF•BE,
即
=
,
而∠OBF=∠EBD,
∴△BOF∽△BED;
(2)∵BC=CD=6,
而DE=CE,
∴DE=4,CE=2,
在Rt△BCE中,BE=
=2
,
在Rt△OBC中,OB=
BC=3
,
∵△BOF∽△BED,
∴
=
,即
=
,
∴OF=
.
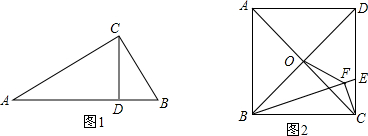
证明:如图1,
∵CD⊥AB,
∴∠ADC=90°,
而∠CAD=∠BAC,
∴Rt△ACD∽Rt△ABC,
∴AC:AB=AD:AC,
∴AC2=AD•AB;
【结论运用】
(1)证明:如图2,
∵四边形ABCD为正方形,
∴OC⊥BO,∠BCD=90°,
∴BC2=BO•BD,
∵CF⊥BE,
∴BC2=BF•BE,
∴BO•BD=BF•BE,
即
| BO |
| BE |
| BF |
| BD |
而∠OBF=∠EBD,
∴△BOF∽△BED;
(2)∵BC=CD=6,
而DE=CE,
∴DE=4,CE=2,
在Rt△BCE中,BE=
| 22+62 |
| 10 |
在Rt△OBC中,OB=
| ||
| 2 |
| 2 |
∵△BOF∽△BED,
∴
| OF |
| DE |
| BO |
| BE |
| OF |
| 4 |
3
| ||
2
|
∴OF=
6
| ||
| 5 |
看了 问题情境如图1,Rt△ABC...的网友还看了以下:
如果在 数轴上A点和B点对应的数为a和 b,且A在原点的左边、B在原点的右边那么a-b是 什么数? 2020-04-05 …
已知下列命题:①若R,且kb=0,则k=-0或b=0;②若a·b=0,则a=0或b=0;③若不平行 2020-04-08 …
已知向量a=(根号3,1)且向量b与a的夹角为30度,求b向量a,b满足:/a向量-b向量/=5a 2020-05-14 …
已知aΔb=(a-b)2,a※b=(a+b)(a-b),例如,1Δ2=(1-2)2=1,1※2=( 2020-05-15 …
几道数学题,厉害来!一.代数式3m+2n可以表示什么二.2a-b除以a+b的意义是()A.a与b差 2020-06-03 …
当a、b满足什么条件时,下列关系成立:(1)|a+b|=|a|+|b|;(2)|a+b|=||a| 2020-06-12 …
定义一种运算“∧”,对于任意两个正数a和b,有a∧b=a+b分之ab.1.验证∧是否具有交换律结合 2020-06-27 …
因式分解公式,请尽可能全面我需要的形式平方差公式:a^2-b^2=(a+b)(a-b); 完全平方 2020-06-27 …
设A,B为同阶方阵,且通过初等变换可以化成相同的标准形,则:A.A和B的秩相等.B.A与B合同设A 2020-06-30 …
(a+b—c)(a—b+c)+(b—a+c)(b—a—c)因式分解的结果是A2b(b—c)(b—a 2020-07-09 …