早教吧作业答案频道 -->数学-->
定义已知P为△ABC所在平面内一点,连接PA,PB,PC,在△PAB,△PBC和△PAC中,若存在一个三角形与△ABC相似(全等除外),那么就称P为△ABC的“共相似点”,根据“共相似点”是否落在
题目详情
【定义】已知P为△ABC所在平面内一点,连接PA,PB,PC,在△PAB,△PBC和△PAC中,若存在一个三角形与△ABC相似(全等除外),那么就称P为△ABC的“共相似点”,根据“共相似点”是否落在三角形的内部,边上或外部,可将其分为“内共相似点”,“边共相似点”或“外共相似点”.
(1)据定义可知,等边三角形___(填“存在”或“不存在”)共相似点.
【探究1】用边共相似点探究三角形的形状
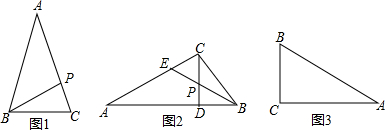
(2)如图1,若△ABC的一个边共相似点P与其对角顶点B的连线,将△ABC分割成的两个三角形恰与原三角形均相似,试判断△ABC的形状,并说明理由.
【探究2】用内共相似点探究三角形的内角关系
(3)如图2,在△ABC中,∠A<∠B<∠C,高线CD与角平分线BE交于点P,若P是△ABC的一个内共相似点,试说明点E是△ABC的边共相似点,并直接写出∠A的度数.
【探究3】探究直角三角形共相似点的个数
(4)如图3,在Rt△ABC中,∠C=90°,∠A=30°,BC=
,若△PBC与△ABC相似,则满足条件的P点共有___个,顺次连接所有满足条件的P点而围成的多边形的周长为___.
(1)据定义可知,等边三角形___(填“存在”或“不存在”)共相似点.
【探究1】用边共相似点探究三角形的形状
(2)如图1,若△ABC的一个边共相似点P与其对角顶点B的连线,将△ABC分割成的两个三角形恰与原三角形均相似,试判断△ABC的形状,并说明理由.
【探究2】用内共相似点探究三角形的内角关系
(3)如图2,在△ABC中,∠A<∠B<∠C,高线CD与角平分线BE交于点P,若P是△ABC的一个内共相似点,试说明点E是△ABC的边共相似点,并直接写出∠A的度数.
【探究3】探究直角三角形共相似点的个数
(4)如图3,在Rt△ABC中,∠C=90°,∠A=30°,BC=
| | 3 |

▼优质解答
答案和解析
(1)根据“共相似点”的定义得:等边三角形不存在共相似点.
故答案为:不存在;
(2)△ABC是直角三角形,理由如下:
根据题意得:△ABP∽△ACB,
∴∠ABP=∠C,
同理得:∠CBP=∠A,
∴∠ABC=∠A+∠C=180°-∠ABC,
解得:∠ABC=90°,
∴△ABC是直角三角形;
(3)根据题意得:△PBC∽△CAB,
∴∠PBC=∠A,∠PCB=∠ABC,
∵BE平分∠ABC,
∴∠ABE=∠PBC,
∴∠A=∠ABE=∠PBC,
∴∠PCB=∠ABC=2∠A=2∠PBC,
∵∠BCE=∠ACB,∠PBC=∠A,
∴△BEC∽△ABC,
∴点E是△ABC的边共相似点;
∵CD是△ABC的高,
∴∠CDB=90°,
∴∠PCB+∠ABC=90°,
∴2∠A+2∠A=90°,
解得:∠A=22.5°;
(4)作CP⊥AB于P,则P为△ABC的“共相似点”;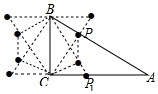
过B作BC的垂线与CP的延长线的交点是△ABC的“共相似点”;
作∠ABC的平分线与AC的交点P1是△ABC的“共相似点”;
过C作BP1的垂线,垂足是△ABC的“共相似点”;
同理:以上四个△ABC的“共相似点”关于直线BC的对称点是△ABC的“共相似点”;
∴△ABC的“共相似点”共有8个,如图所示:
根据等边三角形的性质和直角三角形的性质得:顺次连接所有满足条件的P点而围成的多边形的周长为 2×2+4×
+2×
=6+
;
故答案为:8;6+
.
故答案为:不存在;
(2)△ABC是直角三角形,理由如下:
根据题意得:△ABP∽△ACB,
∴∠ABP=∠C,
同理得:∠CBP=∠A,
∴∠ABC=∠A+∠C=180°-∠ABC,
解得:∠ABC=90°,
∴△ABC是直角三角形;
(3)根据题意得:△PBC∽△CAB,
∴∠PBC=∠A,∠PCB=∠ABC,
∵BE平分∠ABC,
∴∠ABE=∠PBC,
∴∠A=∠ABE=∠PBC,
∴∠PCB=∠ABC=2∠A=2∠PBC,
∵∠BCE=∠ACB,∠PBC=∠A,
∴△BEC∽△ABC,
∴点E是△ABC的边共相似点;
∵CD是△ABC的高,
∴∠CDB=90°,
∴∠PCB+∠ABC=90°,
∴2∠A+2∠A=90°,
解得:∠A=22.5°;
(4)作CP⊥AB于P,则P为△ABC的“共相似点”;

过B作BC的垂线与CP的延长线的交点是△ABC的“共相似点”;
作∠ABC的平分线与AC的交点P1是△ABC的“共相似点”;
过C作BP1的垂线,垂足是△ABC的“共相似点”;
同理:以上四个△ABC的“共相似点”关于直线BC的对称点是△ABC的“共相似点”;
∴△ABC的“共相似点”共有8个,如图所示:
根据等边三角形的性质和直角三角形的性质得:顺次连接所有满足条件的P点而围成的多边形的周长为 2×2+4×
| 1 |
| 2 |
| ||
| 2 |
| 3 |
故答案为:8;6+
| 3 |
看了 定义已知P为△ABC所在平面...的网友还看了以下:
已知两条相交直线a,b,a∥平面α,则b与α的位置关系是()A.b垂直平面αB.b与平面α相交C. 2020-05-13 …
如图所示,L形木板A放在固定的表面粗糙的斜面上,滑块B至于木板上表面,若A B 一起沿如图所示,L 2020-05-17 …
设平面α⊥平面β,在平面α内的一条直线a垂直于平面β内的一条直线b,则A.直线a必垂直于平面βB. 2020-06-15 …
怎么判断向量是否共面?例如下面这题需要判断选项中的项量是否共面:若{a,b,c}构成空间的一个基底 2020-06-22 …
若a,b是空间两条不相交的直线,a属于平面α,b属于平面β,且α‖β,a,b的距离为h1,α,β的 2020-06-27 …
五年级数学简易方程两面三角形的旗子,其中A面旗的底是B面旗对应底的2倍,A面旗底上的高是B面旗对应 2020-06-27 …
(2008•朝阳区二模)如图所示,A、B两个长方体叠放在水平地面上,已知B所受的重力是A的三倍,A 2020-07-07 …
下列命题中,真命题的个数是()①a∥b,a,c异面,则b、c异面②a,b共面,b、c异面,则a、c 2020-08-01 …
一块三角形木块B静止在水平桌面上,而长方形木块A静止在B的斜面上,如图,下列说法正确的是(A.水平桌 2020-11-02 …
平面A垂直于平面B,并交于直线L.a、b分别是面A、B上的点,但都不在L上.连接ab,求a与b分别与 2020-11-28 …