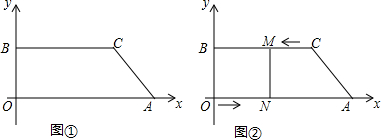
在平面直角坐标系中，点A、B的坐标分别为（a，0），（0，b），其中a，b满足a-2b-18+|2a-5b-30|=0．将点B向右平移26个单位长度得到点C，如图①所示．（1）求点A，B，C的坐标；（2）点M，N分别为

Question

在平面直角坐标系中，点A、B的坐标分别为（a，0），（0，b），其中a，b满足√(a-2b-18)+|2a-5b-30|=0．将点B向右平移26个单位长度得到点C，如图①所示．
（1）求点A，B，C的坐标；
（2）点M，N分别为线段BC，OA上的两个动点，点M从点C向左以1.5个单位长度/秒运动，同时点N从点O向点A以2个单位长度/秒运动，如图②所示，设运动时间为t秒（0<t<15）．
①当CM<AN时，求t的取值范围；
②是否存在一段时间，使得S_{四边形MNOB}>2S_{四边形MNAC}？若存在，求出t的取值范围；若不存在，说明理由．

Answer 1

（1）∵√(a-2b-18)+|2a-5b-30=0，且√(a-2b-18)≥0，|2a-5b-30|≥0，
∴

a-2b-18=0

2a-5b-30=0

，解得：

a=30

b=6

，
∴A（30，0），B（0，6），
又∵点C是由点B向右平移26个单位长度得到，
∴C（26，6）；
（2）①由（1）可知：OA=30，
∵点M从点C向右以1.5个单位长度/秒运动，点N从点O向点A以2个单位长度/秒运动，
∴CM=1.5t，ON=2t，
∴AN=30-2t
∵CM<AN，
∴1.5t<30-2t，解得t<(60)/(7)，而0<t<15，
∴0<t<(60)/(7)；
②由题意可知CM=1.5t，ON=2t，
∴BM=BC-CM=26-1.5t，AN=30-2t，
又B（0，6），
∴OB=6，
∴S_{四边形MNOB}=(1)/(2)OB（BM+ON）=3（26-1.5t+2t）=3（26+0.5t），S_{四边形MNAC}=(1)/(2)OB（AN+CM）=3（30-2t+1.5t）=3（30-0.5t），
当S_{四边形MNOB}>2S_{四边形MNAC}时，则有3（26+0.5t）>2×3（30-0.5t），解得t>(68)/(3)>15，
∴不存在使S_{四边形MNOB}>2S_{四边形MNAC}的时间段．