早教吧作业答案频道 -->数学-->
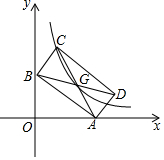
如图,矩形ABCD的两个顶点A、B分别落在x、y轴上,顶点C、D位于第一象限,且OA=3,OB=2,对角线AC、BD交于点G,若曲线y=kx(x>0)经过点C、G,则k=.
题目详情
如图,矩形ABCD的两个顶点A、B分别落在x、y轴上,顶点C、D位于第一象限,且OA=3,OB=2,对角线AC、BD交于点G,若曲线y=
(x>0)经过点C、G,则k=___.
| k |
| x |

▼优质解答
答案和解析
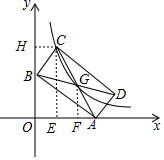 如图,分别过C、G两点作x轴的垂线,交x轴于点E、F,
如图,分别过C、G两点作x轴的垂线,交x轴于点E、F,
∴CE∥GF,
设C(m.n),
∵四边形ABCD是矩形,
∴AG=CG,
∴GF=
CE,EF=
(3-m),
∴OF=
(3-m)+m=
+
m,
∴G(
,
n),
∵曲线y=
(x>0)经过点C、G,
∴mn=
×
n,
解得m=1,
作CH⊥y轴于H,
∴CH=1,
∵∠ABC=90°,
∴∠CBH+∠ABO=90°,
∵∠OAB+∠ABO=90°,
∴∠OAB=∠CBH,
∵∠AOB=∠BHC=90°,
∴△AOB∽△BHC,
∴
=
,即
=
,
∴BH=
,
∴OH=
+2=
,
∴C(1,
),
∴k=1×
=
;
故答案为
.
 如图,分别过C、G两点作x轴的垂线,交x轴于点E、F,
如图,分别过C、G两点作x轴的垂线,交x轴于点E、F,∴CE∥GF,
设C(m.n),
∵四边形ABCD是矩形,
∴AG=CG,
∴GF=
| 1 |
| 2 |
| 1 |
| 2 |
∴OF=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
∴G(
| 3+m |
| 2 |
| 1 |
| 2 |
∵曲线y=
| k |
| x |
∴mn=
| 3+m |
| 2 |
| 1 |
| 2 |
解得m=1,
作CH⊥y轴于H,
∴CH=1,
∵∠ABC=90°,
∴∠CBH+∠ABO=90°,
∵∠OAB+∠ABO=90°,
∴∠OAB=∠CBH,
∵∠AOB=∠BHC=90°,
∴△AOB∽△BHC,
∴
| BH |
| OA |
| CH |
| OB |
| BH |
| 3 |
| 1 |
| 2 |
∴BH=
| 3 |
| 2 |
∴OH=
| 3 |
| 2 |
| 7 |
| 2 |
∴C(1,
| 7 |
| 2 |
∴k=1×
| 7 |
| 2 |
| 7 |
| 2 |
故答案为
| 7 |
| 2 |
看了 如图,矩形ABCD的两个顶点...的网友还看了以下:
已知线段AB=6,C、D是AB上两点,且AC=DB=1,P是线段CD上一动点,在AB同侧分别作等边 2020-06-20 …
已知线段AB=6,C、D是AB上两点,且AC=DB=1,P是线段CD上一动点,在AB同侧分别作等边 2020-06-20 …
四边形ABCD中,AD=BCE,F分别是AB,CD中点,AD的延长线四边形ABCD中,AD=BC. 2020-07-11 …
已知函数f(x)=ax3+3x2-6ax-11,g(x)=3x2+6x+12,和直线m:y=kx+ 2020-07-17 …
1AB是圆O的直径弦CD垂直AB垂足是P若AP比PB是1:4CD=8AB=?2BDCE是三角形AB 2020-07-30 …
如图,在矩形ABCD中对角线AC、BD相交于点F,延长BC到点E,使得四边形ACED是一个平行四边形 2020-11-01 …
已知点P(x0,y0)和直线kx-y+b=0(由y=kx+b变形而得),则点P到直线kx-y+b=0 2020-11-03 …
已知指数函数y=g(x)满足:g(3)=27,定义域为R的函数f(x)=n-g(x)m+3g(x)是 2020-12-23 …
如图所示,桌面上放着一个通电的环形导线,线圈的重力为G,电流方向如图所示.当在环形线圈的中央放上一条 2020-12-25 …
如图,四边形ABCD是正方形,点G是直线BC上的任意一点,DE⊥AG于点E,BF∥DE,交AG于F. 2020-12-25 …