早教吧作业答案频道 -->数学-->
已知在平行四边形ABCD中,AE⊥BC于E点,DF平分∠ADC交线段AE于F点.(1)如图1,若AE=AD,求证:CD=AF+BE;(2)如图2,若AE:AD=a:b,试探究线段CD、AF、BE之间所满足的等量关系,请直接写出你
题目详情
已知在平行四边形ABCD中,AE⊥BC于E点,DF平分∠ADC 交线段AE于F点.
(1)如图1,若AE=AD,求证:CD=AF+BE;
(2)如图2,若AE:AD=a:b,试探究线段CD、AF、BE之间所满足的等量关系,请直接写出你的结论.
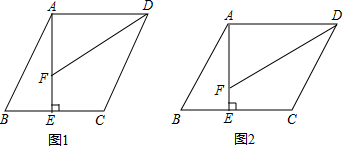
(1)如图1,若AE=AD,求证:CD=AF+BE;
(2)如图2,若AE:AD=a:b,试探究线段CD、AF、BE之间所满足的等量关系,请直接写出你的结论.

▼优质解答
答案和解析
(1)证明:延长EA到G,使得AG=BE,连接DG,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,AD=BC,
∵AE⊥BC于点E,
∴∠AEB=∠AEC=90°,
∴∠AEB=∠DAG=90°,
∴∠DAG=90°,
在△ABE和△DGA中
,
∴△ABE≌△DGA,
∴∠1=∠2,DG=AB,∠B=∠G,
∵四边形ABCD是平行四边形,
∴∠B=∠ADC,
∵∠B+∠1=∠ADC+∠2=90°,∠3=∠4,
∴∠GDF=90°-∠4,∠GFD=90°-∠3,
∴∠GDF=∠GFD,
∴GF=GD=AB=CD,
∵GF=AF+AG=AF+BE,
∴CD=AF+BE;
(2)bCD=aAF+bBE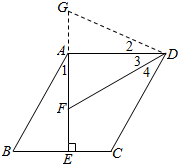
理由是:延长EA到G,使得
=
,连接DG,
即AG=
BE,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,AD=BC,
∵AE⊥BC于点E,
∴∠AEB=∠AEC=90°,
∴∠AEB=∠DAG=90°,
∴∠DAG=90°,
即∠AEB=∠GAD=90°,
∵
=
=
,
∴△ABE∽△DGA,
∴∠1=∠2,
=
,
∴∠GFD=90°-∠3,
∵DF平分∠ADC,
∴∠3=∠4,
∴∠GDF=∠2+∠3=∠1+∠4=180°-∠FAD-∠3=90°-∠3.
∴∠GDF=∠GFD,
∴DG=GF,
∵
=
,AB=CD(已证),
∴bCD=aDG=a(
BE+AF),
即 bCD=aAF+bBE.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,AD=BC,
∵AE⊥BC于点E,
∴∠AEB=∠AEC=90°,
∴∠AEB=∠DAG=90°,
∴∠DAG=90°,
在△ABE和△DGA中
|
∴△ABE≌△DGA,
∴∠1=∠2,DG=AB,∠B=∠G,
∵四边形ABCD是平行四边形,
∴∠B=∠ADC,
∵∠B+∠1=∠ADC+∠2=90°,∠3=∠4,
∴∠GDF=90°-∠4,∠GFD=90°-∠3,
∴∠GDF=∠GFD,
∴GF=GD=AB=CD,
∵GF=AF+AG=AF+BE,
∴CD=AF+BE;
(2)bCD=aAF+bBE

理由是:延长EA到G,使得
| BE |
| AG |
| a |
| b |
即AG=
| b |
| a |
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,AD=BC,
∵AE⊥BC于点E,
∴∠AEB=∠AEC=90°,
∴∠AEB=∠DAG=90°,
∴∠DAG=90°,
即∠AEB=∠GAD=90°,
∵
| AE |
| AD |
| BE |
| AG |
| a |
| b |
∴△ABE∽△DGA,
∴∠1=∠2,
| AB |
| DG |
| a |
| b |
∴∠GFD=90°-∠3,
∵DF平分∠ADC,
∴∠3=∠4,
∴∠GDF=∠2+∠3=∠1+∠4=180°-∠FAD-∠3=90°-∠3.
∴∠GDF=∠GFD,
∴DG=GF,
∵
| AB |
| DG |
| a |
| b |
∴bCD=aDG=a(
| b |
| a |
即 bCD=aAF+bBE.
看了 已知在平行四边形ABCD中,...的网友还看了以下:
△ABC中,∠ABC=45°,CD垂直AB于D,BD平分∠ABC,且BE⊥AC于E,与CD相交于点F 2020-03-31 …
如图,已知正方体ABCD-A'B'C'D',求证:DB'⊥平面ACD' 有用方向向量和法向量证的方 2020-05-16 …
如果a^2+b^2>c^2+d^2,abcd均大于0.求证a+b>c+d如果a^2+b^2>c^2 2020-06-08 …
已知AC的长为定值,D不属于平面ABC,点M、N分别是ΔDAB和ΔDBC的重心.求证:无论B、D如 2020-07-30 …
证明反比性质和更比性质1.如果a/b=c/d,求证b/a=d/c.2.如果a/b=c/d,求证a/c 2020-10-30 …
下列关于期初余额的描述中,正确的有()。A.所有科目都必须输入期初余额B.红字余额应输人负号C.期初 2020-11-21 …
一、能证明的证明,不能的举反例哦!1、如果a>b,判断a-c与b-c的大小2、如果a>b,cb,c> 2020-11-27 …
湖北教师资格证试讲初中英语是否全部用英语来说课如题,我马上就要参加教师资格证的试讲了,湖北的,我考的 2020-11-28 …
劳动者在试用期间被证明不符合录用条件的,用人单位不需要支付经济补偿金。这句话的意思是不是说,如果试用 2020-12-22 …
如图,△ABC内接于圆O,∠BAC的平分线分别交圆O,BC于点D如图,△ABC内接于圆O,∠BAC的 2021-01-09 …