早教吧作业答案频道 -->数学-->
下列五个函数中:①y=2x;②y=;③y=;④y=;⑤y=cos2x,当0<x1<x2<1时,使恒成立的函数是将正确的序号都填上).
题目详情
下列五个函数中:①y=2 x ;②y=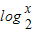 ;③y=
;③y=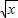 ;④y=
;④y=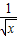 ;⑤y=cos2x,当0<x 1 <x 2 <1时,使
;⑤y=cos2x,当0<x 1 <x 2 <1时,使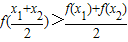 恒成立的函数是 将正确的序号都填上).
恒成立的函数是 将正确的序号都填上).
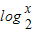 ;③y=
;③y=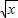 ;④y=
;④y=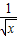 ;⑤y=cos2x,当0<x 1 <x 2 <1时,使
;⑤y=cos2x,当0<x 1 <x 2 <1时,使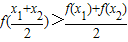 恒成立的函数是 将正确的序号都填上).
恒成立的函数是 将正确的序号都填上).▼优质解答
答案和解析
分析:
因为 恒成立,表示连接两点A(x1,f(x1)),B (x2,f(x2))的线段的中点纵坐标小于f(x)在曲线AB中点(,)的纵坐标,也就是说f(x)的图象“上凸”.所以只需判断哪个函数的图象“上凸”即可.
要使当0<x1<x2<1时,使 恒成立,可得对任意两点A(x1,f(x1)),B (x2,f(x2)),曲线f(x)在A,B两点横坐标的中点的纵坐标,大于A、B两点的纵坐标的一般,也就是说f(x)的图象“上凸”可以画出①②③④⑤的图象进行判断:在0<x1<x2<1上为上凸的图象:可以看见②③的图象是上凸的,对于⑤可以进行研究:y=cos2x,周期T=π,要求在0<x1<x2<1上是上凸的,如上图:在(,1)上是下凹的,在(0,)上是上凸的,故⑤错误;综上:②③是使 恒成立的函数,故答案为:②③;
点评:
此题主要考查指数函数的性质和对数函数的性质,考查的知识点比较全面,利用数形结合的方法会比较简单,是一道好题;
分析:
因为 恒成立,表示连接两点A(x1,f(x1)),B (x2,f(x2))的线段的中点纵坐标小于f(x)在曲线AB中点(,)的纵坐标,也就是说f(x)的图象“上凸”.所以只需判断哪个函数的图象“上凸”即可.
要使当0<x1<x2<1时,使 恒成立,可得对任意两点A(x1,f(x1)),B (x2,f(x2)),曲线f(x)在A,B两点横坐标的中点的纵坐标,大于A、B两点的纵坐标的一般,也就是说f(x)的图象“上凸”可以画出①②③④⑤的图象进行判断:在0<x1<x2<1上为上凸的图象:可以看见②③的图象是上凸的,对于⑤可以进行研究:y=cos2x,周期T=π,要求在0<x1<x2<1上是上凸的,如上图:在(,1)上是下凹的,在(0,)上是上凸的,故⑤错误;综上:②③是使 恒成立的函数,故答案为:②③;
点评:
此题主要考查指数函数的性质和对数函数的性质,考查的知识点比较全面,利用数形结合的方法会比较简单,是一道好题;
看了 下列五个函数中:①y=2x;...的网友还看了以下:
下列句中标点符号使用正确的一项是还有错误的要怎么改?3.下列句中标点符号使用正确的一项是()(2分 2020-06-06 …
求这句话的意思~(必须敢于正视,这才可望敢想、敢说、敢作、敢当.倘使并正视而.)必须敢于正视,这才 2020-06-16 …
下列特称命题中,真命题的个数是()①存在一个实数a使为正整数②存在一个实数x使为正整数③存在一个实 2020-07-29 …
(2011•盐城二模)下列有关动物激素在实践中的应用不正确的是()A.对呆小症患儿注射生长激素使其正 2020-11-12 …
覆盖问题若干个边长为1的正方形尽可能多的填到一个大正方形中,使大正方形的边长最小若干(n个)个边长为 2020-11-24 …
积极情绪的作用有①使人思维敏捷,体力充沛,精力旺盛②有利于个人正确认识事物,分析和解决问题③可以使人 2020-12-01 …
下列各句中,标点符号使用正确的一句是A.叶圣陶先生说过:“标点很重要。一个人标点不大会用,说明他语言 2020-12-04 …
几毫安的电流可以使几伏的小灯泡发光吗?如能如何使其正常工作那就可以使四驱车上的马达正常工作了, 2020-12-08 …
下列各项中,标点符号使用正确的一项是()A.培根说:“读史使人明智;读诗使人灵秀;数学使人精细;物理 2020-12-19 …
下列各句中,标点符号使用正确的一项是()A.培根说:“读史使人明智;读诗使人灵透;数学使人精细;物理 2021-01-15 …