早教吧作业答案频道 -->数学-->
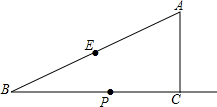
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,点P是射线BC上的一个动点,连接AP、PE,将△AEP沿着边PE折叠,折叠后得到△EPA′,当折叠后△EPA′与△BEP的重叠部分的面
题目详情
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,点P是射线BC上的一个动点,连接AP、PE,将△AEP沿着边PE折叠,折叠后得到△EPA′,当折叠后△EPA′与△BEP的重叠部分的面积恰好为△ABP面积的四分之一,则此时BP的长为___.

▼优质解答
答案和解析
∵∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,
∴AB=4,AE=
AB=2,BC=2
.
①若PA′与AB交于点F,连接A′B,如图1.
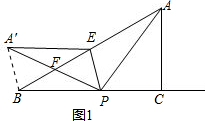
由折叠可得S△A′EP=S△AEP,A′E=AE=2,.
∵点E是AB的中点,
∴S△BEP=S△AEP=
S△ABP.
由题可得S△EFP=
S△ABP,
∴S△EFP=
S△BEP=
S△AEP=
S△A′EP,
∴EF=
BE=BF,PF=
A′P=A′F.
∴四边形A′EPB是平行四边形,
∴BP=A′E=2;
②若EA′与BC交于点G,连接AA′,交EP与H,如图2.
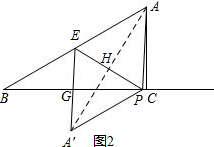 .
.
同理可得GP=
BP=BG,EG=
EA′=
×2=1.
∵BE=AE,∴EG=
AP=1,
∴AP=2=AC,
∴点P与点C重合,
∴BP=BC=2
.
故答案为2或2
.
∴AB=4,AE=
| 1 |
| 2 |
| 3 |
①若PA′与AB交于点F,连接A′B,如图1.

由折叠可得S△A′EP=S△AEP,A′E=AE=2,.
∵点E是AB的中点,
∴S△BEP=S△AEP=
| 1 |
| 2 |
由题可得S△EFP=
| 1 |
| 4 |
∴S△EFP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形A′EPB是平行四边形,
∴BP=A′E=2;
②若EA′与BC交于点G,连接AA′,交EP与H,如图2.
 .
.同理可得GP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵BE=AE,∴EG=
| 1 |
| 2 |
∴AP=2=AC,
∴点P与点C重合,
∴BP=BC=2
| 3 |
故答案为2或2
| 3 |
看了 如图,在Rt△ABC中,∠A...的网友还看了以下:
关于e^cosx的马克老林展开,要求展到X^4项,教材上这样做:e^cosx=e*e^(cosx- 2020-05-17 …
设a>0,f(x)=e^x/a+a/e^x是R上的偶函数,求a值.∵f(x)=e^x/a+a/e^ 2020-05-17 …
在以下给出的表达式中,与while(E)中的(E)不等价的表达式是A)(!E==0)B)(E>0‖ 2020-06-15 …
复变函数反三角函数由z=sinw=[(e^iw)-(e^-iw)]/(2i)得(e^iw)-2iz 2020-07-15 …
已知点A(10,0),B(10,8),C(5,0),D(0,8),E(0,0),(请看补充问题,位 2020-07-30 …
有方程怎么做出曲线来!有这么两个方程y=6.34[1-e^-0.2372(t+0.4045)]其中 2020-08-02 …
惫设f(x)=-m(m+e)x2,g(x)=x2+(m-1)x-m,其中e均自然对数的底数,若∃x 2020-08-02 …
n阶方阵A满足A^2=O,E是n阶单位阵,则A.|E-A|≠0,但|E+A|=0B|E-An阶方阵A 2020-11-02 …
假设股票A和股票B的预期收益和标准差分别为E(RA)=0.15,E(RB)=0.25,σA=0.1σ 2020-11-06 …
变化磁场激发的感应电场满足?如题A.▽·E=0▽×E=0B.▽·E=ρ/ε0▽×E=0C.▽·E=0 2020-12-27 …