早教吧作业答案频道 -->数学-->
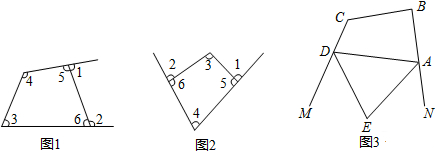
(1)如图1、2,试研究其中∠1、∠2与∠3、∠4之间的数量关系;(2)用你发现的结论解决下列问题:如图3,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.
题目详情
(1)如图1、2,试研究其中∠1、∠2与∠3、∠4之间的数量关系;
(2)用你发现的结论解决下列问题:
如图3,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.
(2)用你发现的结论解决下列问题:
如图3,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.

▼优质解答
答案和解析
(1) ∵∠3、∠4、∠5、∠6是四边形的四个内角,
∴∠3+∠4+∠5+∠6=360°,
∴∠3+∠4=360°-(∠5+∠6),
∵∠1+∠5=180°,∠2+∠6=180°,
∴∠1+∠2=360°-(∠5+∠6),
∴∠1+∠2=∠3+∠4;
(2)答:四边形的任意两个外角的和等于与它们不相邻的两个内角的和;
(3) ∵∠B+∠C=240°,
∴∠MDA+∠NAD=240°,
∵AE、DE分别是∠NAD、∠MDA的平分线,
∴∠ADE=
∠MDA,∠DAE=
∠NAD,
∴∠ADE+∠DAE=
(∠MDA+∠NAD)=
×240°=120°,
∴∠E=180°-(∠ADE+∠DAE)=180°-120°=60°.
∴∠3+∠4+∠5+∠6=360°,
∴∠3+∠4=360°-(∠5+∠6),
∵∠1+∠5=180°,∠2+∠6=180°,
∴∠1+∠2=360°-(∠5+∠6),
∴∠1+∠2=∠3+∠4;
(2)答:四边形的任意两个外角的和等于与它们不相邻的两个内角的和;
(3) ∵∠B+∠C=240°,
∴∠MDA+∠NAD=240°,
∵AE、DE分别是∠NAD、∠MDA的平分线,
∴∠ADE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ADE+∠DAE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠E=180°-(∠ADE+∠DAE)=180°-120°=60°.
看了 (1)如图1、2,试研究其中...的网友还看了以下:
(本小题满分10分)如图,已知反比例函数的图象经过点(,8),直线经过该反比例函数图象上的点Q(4 2020-04-08 …
(2011•成都)如图,已知反比例函数y=kx(k≠0)的图象经过点(12,8),直线y=-x+b 2020-04-08 …
已知直线Y=kx+b,经过点A(0,6)且平行直线Y=-2x,(1)求该函数解析式(2)如果这图爱 2020-04-26 …
下列史实能说明原子核有微观结构的是()A.汤姆孙对阴极射线的研究发现了电子B.卢瑟福的α粒子散射实 2020-05-13 …
在同一直线上的5个点可以确定的线段条数为(),可以确定的射线条数为(),可以确定的直线的条数为() 2020-05-14 …
经线和纬线的形状特征?经线和纬线的位置关系?经线和纬线的长短?经线和纬线的的指示方向?经线和纬线的 2020-05-17 …
总线通常包含地址总线、数据总线和控制总线,其中【】生总线的位数决定了总线的寻址能力。 2020-05-23 …
总线通常包含地址总线、数据总线和控制总线,其中______总线的位数决定了总线的寻址能力。 2020-05-23 …
一道二次函数题目,自我认为很难,请八方相助.已知抛物线y=aX2+bX+c与y轴的交点为C,顶点为 2020-06-07 …
下列叙述中,符合物理学史实的是()A.汤姆孙通过对阴极射线的研究,发现了电子B.卢瑟福通过α粒子的 2020-06-10 …