早教吧作业答案频道 -->数学-->
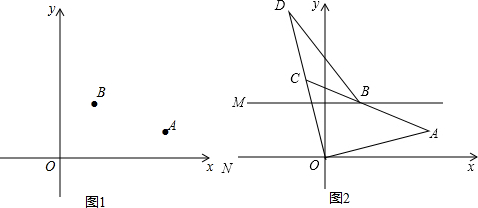
如图1,已知A(a,1),B(2,b),且a,b满足(2a-3b-2)2+a-2b=0.(1)求A,B的坐标;(2)在y轴上是否存在点P,使S△PAB=1?若存在,直接写出满足条件的所有点P的坐标;若不存在,请说明理
题目详情
如图1,已知A(a,1),B(2,b),且a,b满足(2a-3b-2)2+
=0.
(1)求A,B的坐标;
(2)在y轴上是否存在点P,使S△PAB=1?若存在,直接写出满足条件的所有点P的坐标;若不存在,请说明理由.
(3)如图2,MB∥NO,点N在x轴上,OD平分∠AON,延长AB交OD于C,BC平分∠DBM,且∠D+
∠A=60°,求∠DBM的度数.
| a-2b |
(1)求A,B的坐标;
(2)在y轴上是否存在点P,使S△PAB=1?若存在,直接写出满足条件的所有点P的坐标;若不存在,请说明理由.
(3)如图2,MB∥NO,点N在x轴上,OD平分∠AON,延长AB交OD于C,BC平分∠DBM,且∠D+
| 1 |
| 2 |

▼优质解答
答案和解析
 (1)∵a,b满足(2a-3b-2)2+
(1)∵a,b满足(2a-3b-2)2+
=0,
∴
,
解得:
,
∴A(4,1),B(2,2);
(2)由A(4,1),B(2,2)可得
直线AB的解析式为:y=-
x+3,
当x=0时,y=3,
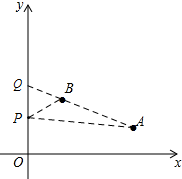
∴直线AB与y轴交于Q(0,3),
设点p的坐标为(0,y),则QP=|y-3|,
当S△PAB=1时,△APQ的面积-△BPQ的面积=1,
即
×|y-3|×4-
×|y-3|×2=1,
解得y=4或2,
所以点P的坐标为(0,4),(0,2);
(3)∵OD平分∠AON,
∴∠1=∠2,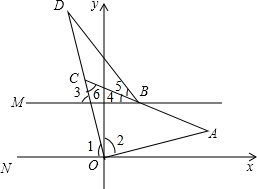
∵AN∥BM,
∴∠1=∠2=∠3=∠4+∠6,
又∵BC平分∠DBM,∠6=∠D+∠5,
∴∠4=∠5=
∠DBM,∠6=∠D+
∠DBM,
∴∠2=∠3=
∠DBM+(∠D+
∠DBM)=∠D+∠DBM,
在△AOC中,∠2+∠6+∠A=180°,
即(∠D+∠DBM)+(∠D+
∠DBM)+∠A=(2∠D+∠A)+
∠DBM=180°,
∵∠D+
∠A=60°,
∴2∠D+∠A=120°,
∴∠DBM=
(180°-120°)=40°.
 (1)∵a,b满足(2a-3b-2)2+
(1)∵a,b满足(2a-3b-2)2+| a-2b |
∴
|
解得:
|
∴A(4,1),B(2,2);
(2)由A(4,1),B(2,2)可得
直线AB的解析式为:y=-
| 1 |
| 2 |
当x=0时,y=3,
∴直线AB与y轴交于Q(0,3),
设点p的坐标为(0,y),则QP=|y-3|,
当S△PAB=1时,△APQ的面积-△BPQ的面积=1,
即
| 1 |
| 2 |
| 1 |
| 2 |
解得y=4或2,
所以点P的坐标为(0,4),(0,2);
(3)∵OD平分∠AON,
∴∠1=∠2,

∵AN∥BM,
∴∠1=∠2=∠3=∠4+∠6,
又∵BC平分∠DBM,∠6=∠D+∠5,
∴∠4=∠5=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠2=∠3=
| 1 |
| 2 |
| 1 |
| 2 |
在△AOC中,∠2+∠6+∠A=180°,
即(∠D+∠DBM)+(∠D+
| 1 |
| 2 |
| 3 |
| 2 |
∵∠D+
| 1 |
| 2 |
∴2∠D+∠A=120°,
∴∠DBM=
| 2 |
| 3 |
看了 如图1,已知A(a,1),B...的网友还看了以下:
有5个人拿着不同的水桶在一个水龙头前排队打水,前面的人接满后离开,后面的人才能继续接水.甲接满水需 2020-05-05 …
已知空间直角坐标系O-XYZ中的点A(1,1,1),平面α过点A且与直线OA垂直,动点P(X,Y, 2020-05-16 …
在平面直角坐标系中,知点A(0,4),B(4,0),P为函数y=8/x(x>0)图象上一点,过点P 2020-06-14 …
已知点P(X,Y)的横,纵坐标满足x+y=5,在平面直角坐标系中标出满足要求的5个点,并观察这5个 2020-06-14 …
点m(x,y)在第一象限,它的坐标满足x+2y=m+2,4x+5y=6m+3,并且x>y点M(x, 2020-06-24 …
坐标系求点的点应该很简单可是好几年没有碰过书本了希望大家帮忙解决下已知坐标系一点P点坐标由坐标系0 2020-07-08 …
已知双曲线C:x^2/3-y^2=1的左,右焦点分别为F1,F2(1)求C上满足向量PF1和向量P 2020-07-26 …
平面坐标几何题求解在直角平面坐标系中,三角形abc的顶点坐标分别是a(1,0),b(-3,0),c 2020-08-02 …
立体几何已知空间直角坐标系Oxyz中的点A(1,1,1),平面a过点A且与直线OA垂直,动点P(x 2020-08-02 …
(本小题满分10分)已知,,点的坐标为(1)当时,求的坐标满足的概率。(2)当时,求的坐标满足的概率 2020-11-01 …