如图，点E在正方形ABCD的对角线AC上，且EC=2AE，直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N．若正方形ABCD的边长为a，则重叠部分四边形EMCN的面积为（）A.23a2B.14a2C.59a2D.49a2

Question

如图，点E在正方形ABCD的对角线AC上，且EC=2AE，直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N．若正方形ABCD的边长为a，则重叠部分四边形EMCN的面积为（　　）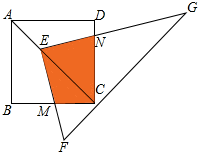

A.

(2)/(3)a²

B.

(1)/(4)a²

C.

(5)/(9)a²

D.

(4)/(9)a²

Answer 1

过E作EP⊥BC于点P，EQ⊥CD于点Q，

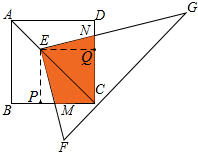
∵四边形ABCD是正方形，
∴∠BCD=90°，
又∵∠EPM=∠EQN=90°，
∴∠PEQ=90°，
∴∠PEM+∠MEQ=90°，
∵三角形FEG是直角三角形，
∴∠NEF=∠NEQ+∠MEQ=90°，
∴∠PEM=∠NEQ，
∵AC是∠BCD的角平分线，∠EPC=∠EQC=90°，
∴EP=EQ，四边形PCQE是正方形，
在△EPM和△EQN中，

∠PEM=∠NEQ

EP=EQ

∠EPM=∠EQN

，
∴△EPM≌△EQN（ASA）
∴S_△EQN=S_△EPM，
∴四边形EMCN的面积等于正方形PCQE的面积，
∵正方形ABCD的边长为a，
∴AC=√(2)a，
∵EC=2AE，
∴EC=(2√(2))/(3)a，
∴EP=PC=(2)/(3)a，
∴正方形PCQE的面积=(2)/(3)a×(2)/(3)a=(4)/(9)a²，
∴四边形EMCN的面积=(4)/(9)a²，
故选：D．