早教吧作业答案频道 -->数学-->
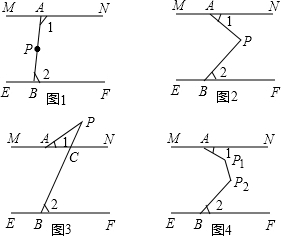
如图1,将两根笔直细木板MN、EF用图钉固定并平行摆放,将一根橡皮筋拉直后用图钉分别固定在MN、EF上,橡皮筋的两端点分别记为点A、点B.(1)图1中,若∠1=110°,则∠2=度.(直接写
题目详情
如图1,将两根笔直细木板MN、EF用图钉固定并平行摆放,将一根橡皮筋拉直后用图钉分别固定在MN、EF上,橡皮筋的两端点分别记为点A、点B.
(1)图1中,若∠1=110°,则∠2=___度.(直接写出结果,不需说理)
(2)P为橡皮筋上一点,利用橡皮筋的弹性拉动橡皮筋,使A、P、B三点不在同一直线上,然后用图钉固定点P.
①如图2,若点P在两细木棒所在直线之间,且∠1+∠2=90°,试判断线段AP与BP所在直线的位置关系,并说明理由;
②如图3,若点P在两细木棒所在直线的同侧,且∠1+∠2=90°,∠APB=28°,试求∠1、∠2的度数.
(3)P1、P2为AB上两点,拉动橡皮筋并固定如图4,若∠1+∠2=90°,则∠AP1P2+∠BP2P1=___度.(直接写出结果,不需说理)
(1)图1中,若∠1=110°,则∠2=___度.(直接写出结果,不需说理)
(2)P为橡皮筋上一点,利用橡皮筋的弹性拉动橡皮筋,使A、P、B三点不在同一直线上,然后用图钉固定点P.
①如图2,若点P在两细木棒所在直线之间,且∠1+∠2=90°,试判断线段AP与BP所在直线的位置关系,并说明理由;
②如图3,若点P在两细木棒所在直线的同侧,且∠1+∠2=90°,∠APB=28°,试求∠1、∠2的度数.
(3)P1、P2为AB上两点,拉动橡皮筋并固定如图4,若∠1+∠2=90°,则∠AP1P2+∠BP2P1=___度.(直接写出结果,不需说理)

▼优质解答
答案和解析
(1)∵MN∥EF,
∴∠1+∠2=180°,
∵∠1=110°,
∴∠2=70°.
故答案为:70.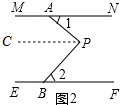
(2)①AP⊥BP,理由如下:
在图2中,过点P作PC∥MN,
∵MN∥EF,
∴PC∥MN∥EF,
∴∠APC=∠1,∠BPC=∠2.
∵∠APB=∠APC+∠BPC,∠1+∠2=90°,
∴∠APB=90°,
∴AP⊥BP.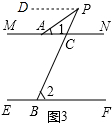
②在图3中,过点P作PD∥MN,
∵MN∥EF,
∴PD∥MN∥EF,
∴∠DPA=∠1,∠DPB=∠2,
∴∠APB=∠DPB-∠DPA=∠2-∠1=28°.
又∵∠1+∠2=90°,
∴∠1=31°,∠2=59°.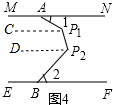
(3)在图4中,过点P1作P1C∥MN,过点P2作P2D∥MN,
∵MN∥EF,
∴P1C∥MN∥EF∥P2D,
∴∠1=∠AP1C,∠2=∠BP2D,∠CP1P2+∠DP2P1=180°.
又∵∠1+∠2=90°,
∴∠AP1P2+∠BP2P1=∠AP1C+∠CP1P2+∠BP2D+∠DP2P1=(∠AP1C+∠BP2D)+(∠CP1P2+∠DP2P1)=90°+180°=270°.
故答案为:270.
∴∠1+∠2=180°,
∵∠1=110°,
∴∠2=70°.
故答案为:70.

(2)①AP⊥BP,理由如下:
在图2中,过点P作PC∥MN,
∵MN∥EF,
∴PC∥MN∥EF,
∴∠APC=∠1,∠BPC=∠2.
∵∠APB=∠APC+∠BPC,∠1+∠2=90°,
∴∠APB=90°,
∴AP⊥BP.

②在图3中,过点P作PD∥MN,
∵MN∥EF,
∴PD∥MN∥EF,
∴∠DPA=∠1,∠DPB=∠2,
∴∠APB=∠DPB-∠DPA=∠2-∠1=28°.
又∵∠1+∠2=90°,
∴∠1=31°,∠2=59°.

(3)在图4中,过点P1作P1C∥MN,过点P2作P2D∥MN,
∵MN∥EF,
∴P1C∥MN∥EF∥P2D,
∴∠1=∠AP1C,∠2=∠BP2D,∠CP1P2+∠DP2P1=180°.
又∵∠1+∠2=90°,
∴∠AP1P2+∠BP2P1=∠AP1C+∠CP1P2+∠BP2D+∠DP2P1=(∠AP1C+∠BP2D)+(∠CP1P2+∠DP2P1)=90°+180°=270°.
故答案为:270.
看了 如图1,将两根笔直细木板MN...的网友还看了以下:
根适于吸水的特点是()A.成熟区有大量的根毛B.分生区细胞不断分裂C.伸长区细胞不断伸长D.根冠有 2020-05-13 …
根尖的成熟区最明显的特点是()A.根部变粗B.有大量根毛C.被根冠包围着D.颜色变深 2020-05-13 …
小李将番茄的幼苗移栽后,开始几天出现了萎蔫现象。造成这一现象的主要原因是()A.损伤了幼根或根毛B 2020-07-06 …
39.水稻种子在氧气供应不足的条件下的萌发特点是39.水稻种子在氧气供应不足的条件下的萌发特点是A 2020-07-17 …
须根系的特点是[]A.没有主根的根系B.主要由不定根组成C.生有须根的根系D.侧根和不定根没有明显区 2020-12-25 …
求详细解答:须根系的特点是须根系的特点是[]A.没有主根的根系B.主要由不定根组成C.生有须根的根系 2020-12-25 …
直根系的特点是()①主根长而粗②主根不发达③侧根短而细④由不定根组成.A.①③B.①②C.②③D.① 2020-12-25 …
(2005•岳阳)池塘边生长着一株水杉,根据根的生长特点分析,靠水的这边()A.根系发达B.根系不发 2020-12-25 …
池塘边生长着一株水杉,根据根的生长特点分析,靠水的这边[]A.根系发达B.根系不发达C.无根系D.根 2020-12-25 …
(2011•绍兴二模)某同学在家中用三根相同的橡皮筋(遵循胡克定律)来探究求合力的方法.如图所示,三 2021-01-15 …