早教吧作业答案频道 -->数学-->
已知:如图,在△ABC中,AB=AC,AD是△ABC的一条角平分线,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.(1)求证:四边形ADCE为矩形;(2)连接DE,交AC于点F,请判断四边形ABDE的形状,
题目详情
已知:如图,在△ABC中,AB=AC,AD是△ABC的一条角平分线,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.
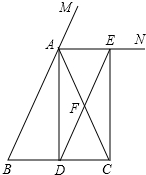
(1)求证:四边形ADCE为矩形;
(2)连接DE,交AC于点F,请判断四边形ABDE的形状,并证明;
(3)线段DF与AB有怎样的关系?请直接写出你的结论.

(1)求证:四边形ADCE为矩形;
(2)连接DE,交AC于点F,请判断四边形ABDE的形状,并证明;
(3)线段DF与AB有怎样的关系?请直接写出你的结论.
▼优质解答
答案和解析
 (1)证明:∵在△ABC中,AB=AC,AD是BC边的中线,
(1)证明:∵在△ABC中,AB=AC,AD是BC边的中线,
∴AD⊥BC,∠BAD=∠CAD,
∴∠ADC=90°,
∵AN为△ABC的外角∠CAM的平分线,
∴∠MAN=∠CAN,
∴∠DAE=90°,
∵CE⊥AN,
∴∠AEC=90°,
∴四边形ADCE为矩形;
(2)四边形ABDE是平行四边形,理由如下:
证明:由(1)知,四边形ADCE为矩形,则AE=CD,AC=DE.
又∵AB=AC,BD=CD,
∴AB=DE,AE=BD,
∴四边形ABDE是平行四边形;
(3)DF∥AB,DF=
AB.理由:
∵四边形ADCE为矩形,
∴AF=CF,
∵BD=CD,
∴DF是△ABC的中位线,
∴DF∥AB,DF=
AB.
 (1)证明:∵在△ABC中,AB=AC,AD是BC边的中线,
(1)证明:∵在△ABC中,AB=AC,AD是BC边的中线,∴AD⊥BC,∠BAD=∠CAD,
∴∠ADC=90°,
∵AN为△ABC的外角∠CAM的平分线,
∴∠MAN=∠CAN,
∴∠DAE=90°,
∵CE⊥AN,
∴∠AEC=90°,
∴四边形ADCE为矩形;
(2)四边形ABDE是平行四边形,理由如下:
证明:由(1)知,四边形ADCE为矩形,则AE=CD,AC=DE.
又∵AB=AC,BD=CD,
∴AB=DE,AE=BD,
∴四边形ABDE是平行四边形;
(3)DF∥AB,DF=
| 1 |
| 2 |
∵四边形ADCE为矩形,
∴AF=CF,
∵BD=CD,
∴DF是△ABC的中位线,
∴DF∥AB,DF=
| 1 |
| 2 |
看了 已知:如图,在△ABC中,A...的网友还看了以下:
两根相同的棒,一根是铁棒,一根是条形磁铁,在没有其他任何工具的情况下怎么辨别它们是否有磁性?两种办 2020-05-14 …
盲道是为盲人提供行路方便和安全的道路设施,一般由两种砖铺成,一种是条形引导砖,引导盲人放心前行,称 2020-06-19 …
盲道是为盲人提供行路方便和安全的道路设施,一般由两种砖铺成,一种是条形引导砖,引导盲人放心前行,称 2020-06-19 …
盲道是为盲人提供行路方便和安全的道路设施,一般由两种砖铺成,一种是条形引导砖,引导盲人放心前行,称 2020-06-19 …
如果否B可以推出否A,那么条件B是条件A成立的条件? 2020-07-09 …
命题“等角的补角相等”中的“等角的补角”是()A.条件部分B.是条件,也是结论 2020-07-30 …
命题的否定:命题若两个角相等,则这两个角是对顶角按照我在学习全称命题的否定之前,我一直是条件不变, 2020-08-01 …
多元函数在某个条件限制下的最值一定是条件极值吗?求出条件极值后是不是还应该验证一下类似单变量函数的" 2020-12-14 …
选出语法分析正确的一项这个也不行,那个也不行,只有自己最行,是一切骄傲的人的共同特点。A.这是一个二 2020-12-24 …
条形统计图大体上分为两种:一种是条形统计图;一种是条形统计图. 2020-12-25 …