如图，△ABC中，∠ABC的角平分线与∠ACB的外角∠ACD的平分线交于A1．（1）当∠A为70°时，∵∠ACD-∠ABD=∠∴∠ACD-∠ABD=°∵BA1、CA1是∠ABC的角平分线与∠ACB的外角∠ACD的平分线∴∠A1CD-

Question

如图，△ABC中，∠ABC的角平分线与∠ACB的外角∠ACD的平分线交于A₁．

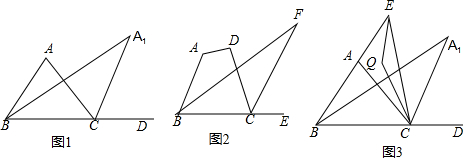
（1）当∠A为70°时，
∵∠ACD-∠ABD=∠___
∴∠ACD-∠ABD=___°
∵BA₁、CA₁是∠ABC的角平分线与∠ACB的外角∠ACD的平分线
∴∠A₁CD-∠A₁BD= (1)/(2)（∠ACD-∠ABD）
∴∠A₁=___°；
（2）∠A₁BC的角平分线与∠A₁CD的角平分线交于A₂，∠A₂BC与A₂CD的平分线交于A₃，如此继续下去可得A₄、…、A_n，请写出∠A与∠A_n的数量关系___；
（3）如图2，四边形ABCD中，∠F为∠ABC的角平分线及外角∠DCE的平分线所在的直线构成的角，若∠A+∠D=230度，则∠F=___．
（4）如图3，若E为BA延长线上一动点，连EC，∠AEC与∠ACE的角平分线交于Q，当E滑动时有下面两个结论：①∠Q+∠A₁的值为定值；②∠Q-∠A₁的值为定值．其中有且只有一个是正确的，请写出正确的结论，并求出其值．

Answer 1

（1）当∠A为70°时，
∵∠ACD-∠ABD=∠A，
∴∠ACD-∠ABD=70°，
∵BA₁、CA₁是∠ABC的角平分线与∠ACB的外角∠ACD的平分线，
∴∠A₁CD-∠A₁BD=(1)/(2)（∠ACD-∠ABD）
∴∠A₁=35°；
故答案为：A，70，35；

（2）∵A₁B、A₁C分别平分∠ABC和∠ACD，
∴∠ACD=2∠A₁CD，∠ABC=2∠A₁BC，
而∠A₁CD=∠A₁+∠A₁BC，∠ACD=∠ABC+∠BAC，
∴∠BAC=2∠A₁=80°，
∴∠A₁=40°，
同理可得∠A₁=2∠A₂，
即∠BAC=2²∠A₂=80°，
∴∠A₂=20°，
∴∠A=2ⁿ∠A_n，即∠A_n=(1)/(2n)∠A，
故答案为：∠A_n=(1)/(2n)∠A．

（3）∵∠ABC+∠DCB=360°-（∠A+∠D），
∴∠ABC+（180°-∠DCE）=360°-（∠A+∠D）=2∠FBC+（180°-2∠DCF）=180°-2（∠DCF-∠FBC）=180°-2∠F，
∴360°-（α+β）=180°-2∠F，
2∠F=∠A+∠D-180°，
∴∠F=(1)/(2)（∠A+∠D）-90°，
∵∠A+∠D=230°，
∴∠F=25°；
故答案为：25°．

（4）①∠Q+∠A₁的值为定值正确．
∵∠ACD-∠ABD=∠BAC，BA₁、CA₁是∠ABC的角平分线与∠ACB的外角∠ACD的平分线
∴∠A₁=∠A₁CD-∠A₁BD=(1)/(2)∠BAC，（1分）
∵∠AEC+∠ACE=∠BAC，EQ、CQ是∠AEC、∠ACE的角平分线，
∴∠QEC+∠QCE=(1)/(2)（∠AEC+∠ACE）=(1)/(2)∠BAC，
∴∠Q=180°-（∠QEC+∠QCE）=180°-(1)/(2)∠BAC，
∴∠Q+∠A₁=180°．