早教吧作业答案频道 -->数学-->
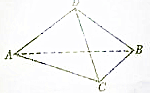
如图所示,把等腰直角三角形ABC沿斜边AB旋转至△ABD的位置,使CD=AC,求证:平面ABD⊥平面ABC.
题目详情
如图所示,把等腰直角三角形ABC沿斜边AB旋转至△ABD的位置,使CD=AC,求证:平面ABD⊥平面ABC.

▼优质解答
答案和解析
证明:取AB中点E,连接DE,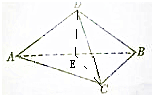
∵△ABD是等腰直角三角形,
∴DE⊥AB,且DE=
,
连接CE,同理CE⊥AB,且CE=
,
∵AD=AC,∴CE=DE=
,
∵CD=AC,∴CE2+DE2=CD2,
∴△CDE为等腰直角三角形,DE⊥CE,
∵AB∩CE于E,∴DE⊥平面ABC,
又∵DE⊂平面ABD,
∴平面ABD⊥平面ABC.

∵△ABD是等腰直角三角形,
∴DE⊥AB,且DE=
| AD | ||
|
连接CE,同理CE⊥AB,且CE=
| AC | ||
|
∵AD=AC,∴CE=DE=
| AC | ||
|
∵CD=AC,∴CE2+DE2=CD2,
∴△CDE为等腰直角三角形,DE⊥CE,
∵AB∩CE于E,∴DE⊥平面ABC,
又∵DE⊂平面ABD,
∴平面ABD⊥平面ABC.
看了 如图所示,把等腰直角三角形A...的网友还看了以下:
如果通过平移直线得到的图象,那么直线必须().A.向上平移5个单位B.向下平移5个单位C.向上平移 2020-05-13 …
如果通过平移直线得到的图象,那么直线必须().A.向上平移5个单位B.向下平移5个单位C.向上平移 2020-05-13 …
质量为m、带电荷量为+q的小球,用一长为l的绝缘细线悬挂在方向垂直纸面向里的匀强磁场中,磁感应强度 2020-05-13 …
平衡位置就是物体振动范围的中心位置关于机械振动的位移和平衡位置,以下说法中正确的是( )A.平衡位 2020-05-14 …
差压液位计的法兰和显示头必须安装在与下端毛细管接口水平的位置吗?如题,如果过高或过低会不会对测量结 2020-05-16 …
急性盆腔炎应采取何种体位( )A.平卧位B.左侧卧位C.头低足高位D.半卧位 2020-06-07 …
为减轻胸膜炎所引起的胸痛应采取何卧位A.平卧位B.患侧卧位C.俯卧位D.半卧位E.健侧卧位 2020-06-07 …
对于左心衰竭患者可使患者症状缓解的措施不包括A:平卧位B:强心剂C:利尿剂D:降压E:坐位 2020-06-07 …
物理高二磁场急一质量为m、带电荷量为+q的小球用一长为L的绝缘细线悬挂在方向垂直纸面向里的匀强磁场 2020-06-10 …
一系列横波沿水平放置的弹性绳向右传播,绳上两质点A、B的平衡位置相距3/4波长,B位于A右方。t时 2020-06-16 …