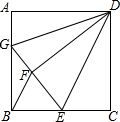
如图，已知正方形ABCD的边长为12，BE=EC，将正方形边CD沿DE折叠到DF，延长EF交AB于G，连接DG，现在有如下4个结论：①△ADG≌△FDG；②GB=2AG；③△GDE∽BEF；④S△BEF=725．在以

Question

如图，已知正方形ABCD的边长为12，BE=EC，将正方形边CD沿DE折叠到DF，延长EF交AB于G，连接DG，现在有如下4个结论：①△ADG≌△FDG；②GB=2AG；③△GDE∽BEF；④S_△BEF= (72)/(5)．在以上4个结论中，其中一定成立的是___（把所有正确结论的序号都填在横线上）

Answer 1

由折叠可知，DF=DC=DA，∠DFE=∠C=90°，
∴∠DFG=∠A=90°，
∴△ADG≌△FDG，①正确；
∵正方形边长是12，
∴BE=EC=EF=6，
设AG=FG=x，则EG=x+6，BG=12-x，
由勾股定理得：EG²=BE²+BG²，
即：（x+6）²=6²+（12-x）²，
解得：x=4
∴AG=GF=4，BG=8，BG=2AG，②正确；
BE=EF=6，△BEF是等腰三角形，易知△GED不是等腰三角形，③错误；
S△GBE=(1)/(2)×6×8=24，S△BEF=(EF)/(EG)•S△GBE=(6)/(10)×24=(72)/(5)，④正确；
故答案为：①，②，④．