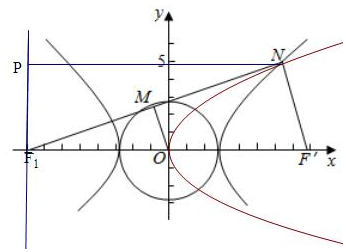
过曲线C1：x2a2-y2b2=1（a>0，b>0）的左焦点F1作曲线C2：x2+y2=a2的切线，设切点为M，延长F1M交曲线C3：y2=2px（p>0）于点N，其中C1，C3有一个共同的焦点，若MF1+MN=0，则曲线C1的离心率为（

Question

过曲线C₁：

(x2)/(a2)-(y2)/(b2)=1（a>0，b>0）的左焦点F₁作曲线C₂：x²+y²=a²的切线，设切点为M，延长F₁M交曲线C₃：y²=2px（p>0）于点N，其中C₁，C₃有一个共同的焦点，若

MF1

+

MN

=

0

，则曲线C₁的离心率为（　　）

A.

(√(5)+1)/(2)

B.

√(5)

C.

(√(2)+1)/(2)

D.

√(2)

Answer 1

设双曲线的右焦点为F'，则F'的坐标为（c，0）
因为曲线C₁与C₃有一个共同的焦点，所以y²=4cx，
因为

MF1

+

MN

=

0

，
所以

MF1

=-

MN

=

NM

，
则M为F₁N的中点，
因为O为F₁F'的中点，M为F₁N的中点，所以OM为△NF₁F'的中位线，
所以OM∥PF'
因为|OM|=a，所以|NF'|=2a
又NF'⊥NF₁，|F₁F'|=2c 所以|NF₁|=2b
设N（x，y），则由抛物线的定义可得x+c=2a，
∴x=2a-c
过点F₁作x轴的垂线，点N到该垂线的距离为2a
由勾股定理 y²+4a²=4b²，即4c（2a-c）+4a²=4（c²-a²）
得e²-e-1=0，
∴e=(√(5)+1)/(2)．
故选：A．