早教吧作业答案频道 -->数学-->
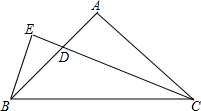
如图,△ABC中,AB=AC,∠BAC=90°,CD平分∠ACB,BE⊥CD,垂足E在CD的延长线上,试探究线段BE和CD的数量关系,并证明你的结论.
题目详情
如图,△ABC中,AB=AC,∠BAC=90°,CD平分∠ACB,BE⊥CD,垂足E在CD的延长线上,试探究线段BE和CD的数量关系,并证明你的结论.

▼优质解答
答案和解析
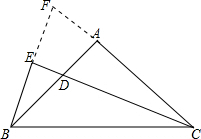 CD=2BE,理由为:
CD=2BE,理由为:
延长BE交CA延长线于F,
∵CD平分∠ACB,
∴∠FCE=∠BCE,
在△CEF和△CEB中,
,
∴△CEF≌△CEB(ASA),
∴FE=BE,
∵∠DAC=∠CEF=90°,
∴∠ACD+∠F=∠ABF+∠F=90°,
∴∠ACD=∠ABF,
在△ACD和△ABF中,
,
∴△ACD≌△ABF(ASA),
∴CD=BF,
∴CD=2BE.
 CD=2BE,理由为:
CD=2BE,理由为:延长BE交CA延长线于F,
∵CD平分∠ACB,
∴∠FCE=∠BCE,
在△CEF和△CEB中,
|
∴△CEF≌△CEB(ASA),
∴FE=BE,
∵∠DAC=∠CEF=90°,
∴∠ACD+∠F=∠ABF+∠F=90°,
∴∠ACD=∠ABF,
在△ACD和△ABF中,
|
∴△ACD≌△ABF(ASA),
∴CD=BF,
∴CD=2BE.
看了 如图,△ABC中,AB=AC...的网友还看了以下:
将下列式子写成(A+B)(A-B)的形式①(-a+b+c-d)(-a-b+c+d)②(a+b将下列 2020-04-27 …
是关于相似图形的性质的题!(1)已知a/b=c/d,求证a+c/b+a=a/b(2)已知a/b=c 2020-05-16 …
设有关系模式R(A,B,C,D,E,F),根据语义有如下函数依赖集:F={A→B,(C,D) →A, 2020-05-24 …
初三比例式计算.如题.已知a/b=c/d(bd不等于0).判断下列比例式是否成立.并说明理由.a- 2020-06-10 …
①.113÷a=b余c,被错算成131÷a,结果商是b+3余数仍是c,求c是几?②.已知a÷b=c 2020-07-18 …
如果ABCD代表不同的自然数A\B×C\D相等的是选择题这是选项A.C\A×D\BB.A\B×D\ 2020-07-26 …
1.已知a比b=c比d,写出以a和d为内项的比例式;写出以a和d为外项的比例式..2.已知ad=b 2020-08-02 …
读“丹霞地貌形成示意图”,回答下列各题:1.丹霞地貌的形成过程正确的是()A.c→b→d→a→f→e 2020-11-21 …
丹霞地貌的形成过程正确的是()A.c→b→d→a→f→eB.b→a→c→d→f→eC.a→h→c→d 2020-11-21 …
代数化简法化简1.L=A*B*非C+非(A*B*C)*非(A*B)1.L=A*B*非C+非(A*B* 2020-12-07 …