早教吧作业答案频道 -->数学-->
如图,四边形ABCD为矩形,E为BC边中点,以AD为直径的O与AE交于点F.(1)求证:四边形AOCE为平行四边形;(2)求证:CF与O相切;(3)若F为AE的中点,求∠ADF的大小.
题目详情
如图,四边形ABCD为矩形,E为BC边中点,以AD为直径的 O与AE交于点F.

(1)求证:四边形AOCE为平行四边形;
(2)求证:CF与 O相切;
(3)若F为AE的中点,求∠ADF的大小.

(1)求证:四边形AOCE为平行四边形;
(2)求证:CF与 O相切;
(3)若F为AE的中点,求∠ADF的大小.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,∠ADC=90°,
∵E为BC边中点,AO=DO,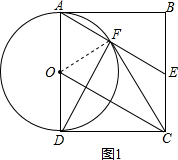
∴AO=
AD,EC=
BC,
∴AO=EC,AO∥EC,
∴四边形OAEC是平行四边形;
(2)如图1,连接OF,
∵四边形OAEC是平行四边形
∴AE∥OC,
∴∠DOC=∠OAF,
∠FOC=∠OFA,
∵OA=OF,
∴∠OAF=∠OFA,
∴∠DOC=∠FOC,
在△ODC与△OFC中,
,
∴△ODC≌△OFC(SAS),
∴∠OFC=∠ODC=90°,
∴OF⊥CF,
∴CF与 O相切;
(3)如图2,连接DE,
∵AD是直径,
∴∠AFD=90°,
∵点F为AE的中点,
∴DF为AE的垂直平分线,
∴DE=AD,
在△ABE与R△DCE中,
,
∴△ABE≌△DCE,
∴AE=DE,
∴AE=DE=AD,
∴三角形ADE为等边三角形,
∴∠DAF=60°,
∴∠ADF=30°.
∴AD∥BC,AD=BC,∠ADC=90°,
∵E为BC边中点,AO=DO,

∴AO=
| 1 |
| 2 |
| 1 |
| 2 |
∴AO=EC,AO∥EC,
∴四边形OAEC是平行四边形;
(2)如图1,连接OF,
∵四边形OAEC是平行四边形
∴AE∥OC,
∴∠DOC=∠OAF,
∠FOC=∠OFA,
∵OA=OF,
∴∠OAF=∠OFA,

∴∠DOC=∠FOC,
在△ODC与△OFC中,
|
∴△ODC≌△OFC(SAS),
∴∠OFC=∠ODC=90°,
∴OF⊥CF,
∴CF与 O相切;
(3)如图2,连接DE,
∵AD是直径,
∴∠AFD=90°,
∵点F为AE的中点,
∴DF为AE的垂直平分线,
∴DE=AD,
在△ABE与R△DCE中,
|
∴△ABE≌△DCE,
∴AE=DE,
∴AE=DE=AD,
∴三角形ADE为等边三角形,
∴∠DAF=60°,
∴∠ADF=30°.
看了 如图,四边形ABCD为矩形,...的网友还看了以下:
ABCDEF乘4=EFABCD,求A,B,C,D,E,F的值A,B,C,D,E,F各表示一个数 2020-05-16 …
已知A,B,C,D,E,F是含有同一种元素的化合物,其中F能使红色石蕊试纸变蓝色,它们之间能发生如 2020-05-20 …
某次考试A,B,C,D,E五人的平均数比C,D,E,F的平均分少6分,A,B两人的平均数是80,求 2020-05-20 …
若(3x-2)^6=ax^6+bx^5+cx^4.若(3x-2)^6=ax^6+bx^5+cx^4 2020-05-21 …
如图所示,杯子放在水平地面上,对水平地面有力F作用,则下面说法正确的是()A.力F的性质是压力B. 2020-05-24 …
如图所示,杯子放在水平地面上,对水平地面有力F作用,则下面说法正确的是()A.力F的性质是压力B. 2020-05-24 …
设(2x-1)5次方=ax5次方+bx4次方+cx3次方+dx2次方+es+f求f的值?求a+b+ 2020-06-03 …
已知:a、b、c、d、e、f均为常数,且对任意实数x,等式(3x+1)的5次方=ax的5次方+bx 2020-06-03 …
数学五元一次方程求解a+b+c+d+f=116a+8b+4c+2d+f=981a+27b+9c+3 2020-06-11 …
D具有酸性,F具有中性,在D和F中加酸和高锰酸钾共热时,都被氧化放出CO2,求D和F的结构式,D和 2020-06-12 …