早教吧作业答案频道 -->数学-->
如图,在四棱锥S-ABCD中,底面ABCD为菱形,E、P、Q分别是棱AD、SC、AB的中点,且SE⊥平面ABCD.(1)求证:PQ∥平面SAD;(2)求证:平面SAC⊥平面SEQ.
题目详情
如图,在四棱锥S-ABCD中,底面ABCD为菱形,E、P、Q分别是棱AD、SC、AB的中点,且SE⊥平面ABCD.
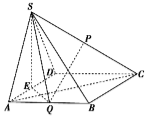
(1)求证:PQ∥平面SAD;
(2)求证:平面SAC⊥平面SEQ.

(1)求证:PQ∥平面SAD;
(2)求证:平面SAC⊥平面SEQ.
▼优质解答
答案和解析
证明: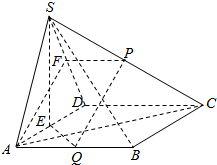 (1)取SD中点F,连结AF,PF.
(1)取SD中点F,连结AF,PF.
因为 P,F分别是棱SC,SD的中点,
所以 FP∥CD,且FP=
CD.
又因为菱形ABCD中,Q是AB的中点,
所以 AQ∥CD,且AQ=
CD.
所以 FP∥AQ且FP=AQ.
所以 AQPF为平行四边形.
所以 PQ∥AF.
又因为 PQ⊄平面SAD,
AF⊂平面SAD,
所以 PQ∥平面SAD;
(2)连结BD,
因为△SAD中SA=SD,点E棱AD的中点,
所以 SE⊥AD,
又 平面SAD⊥平面ABCD,
平面SAD∩平面ABCD=AD,
SE⊂平面SAD,
所以 SE⊥平面ABCD,
所以SE⊥AC.
因为 底面ABCD为菱形,
E,Q分别是棱AD,AB的中点,
所以 BD⊥AC,EQ∥BD.
所以 EQ⊥AC,
因为 SE∩EQ=E,
所以 AC⊥平面SEQ.
因为AC⊂平面SAC,所以平面SAC⊥平面SEQ.
 (1)取SD中点F,连结AF,PF.
(1)取SD中点F,连结AF,PF.因为 P,F分别是棱SC,SD的中点,
所以 FP∥CD,且FP=
| 1 |
| 2 |
又因为菱形ABCD中,Q是AB的中点,
所以 AQ∥CD,且AQ=
| 1 |
| 2 |
所以 FP∥AQ且FP=AQ.
所以 AQPF为平行四边形.
所以 PQ∥AF.
又因为 PQ⊄平面SAD,
AF⊂平面SAD,
所以 PQ∥平面SAD;
(2)连结BD,
因为△SAD中SA=SD,点E棱AD的中点,
所以 SE⊥AD,
又 平面SAD⊥平面ABCD,
平面SAD∩平面ABCD=AD,
SE⊂平面SAD,
所以 SE⊥平面ABCD,
所以SE⊥AC.
因为 底面ABCD为菱形,
E,Q分别是棱AD,AB的中点,
所以 BD⊥AC,EQ∥BD.
所以 EQ⊥AC,
因为 SE∩EQ=E,
所以 AC⊥平面SEQ.
因为AC⊂平面SAC,所以平面SAC⊥平面SEQ.
看了 如图,在四棱锥S-ABCD中...的网友还看了以下:
是否存在常数p、q,使得x的四次方+p(x)的平方+q能被x的平方+2x+5整除?存在,请求出p、 2020-05-16 …
已知集合P={a,a+d,a+2d},Q={a,aq,aq^2},其中a≠0,且P=Q,求q的值. 2020-05-17 …
若(p-q)的平方-(q-p)的立方=(q-p)的平方再乘以E则E是(1+p-q)求解答过程会有加 2020-05-20 …
平面上有四点A、B、Q、P,其中A、B为定点,且|AB|=3,P、Q为动点,满足|AP|=|PQ| 2020-05-23 …
设函数Q(x,y)在平面xOy上具有一阶连续偏导数,曲线积分∫L2xydx+Q(x,y)dy与路径 2020-06-11 …
如何解释最佳订货批量的公式:Q*=Squat(2DC/H)Squat()函数表示开平方根.R=LT 2020-07-10 …
2d+q的四次方=20,4d+q的平方=12,求d和q2d+q的四次方=20,4d+q的平方=13 2020-07-14 …
(1)已知抛物线y=2x2,把它向右平移p个单位,或向下平移q个单位,都能使得抛物线与直线y=x- 2020-08-02 …
两个相对的平行电极板,已知电荷量和板间距怎么求场强和电势差两个相对的平行电极板,已知两个电极板所带相 2020-10-31 …
高一数学,帮解下,谢谢已知M={a,a+d,a+2d}.N={a,aq,a乘以(q的平方)},a不等 2020-11-27 …