早教吧作业答案频道 -->数学-->
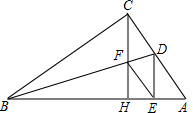
如图所示,△ABC中,∠ACB=90°,∠ABC的平分线BD交AC于点D,CH⊥AB于H,且交BD于点F,DE⊥AB于E,四边形CDEF是菱形吗?请说明理由.
题目详情
如图所示,△ABC中,∠ACB=90°,∠ABC的平分线BD交AC于点D,CH⊥AB于H,且交BD于点F,DE⊥AB于E,四边形CDEF是菱形吗?请说明理由.

▼优质解答
答案和解析
四边形CDEF是菱形.理由如下:
∵△ABC中,∠ACB=90°,
∴DC⊥CB,
又∵DE⊥AB于E,且∠ABC的平分线BD交AC于点D,
∴CD=DE(角平分线上的点到角的两边的距离相等)
在△CBD与△EBD中,
∴△CBD≌△EBD
∴∠CDF=∠EDF
又在△CDF与△EDF中,
∴△CDF≌△EDF
∴∠FCD=∠FED
又CH⊥AB于H,且交BD于点F,DE⊥AB于E,
∴CF∥DE,∠HFE=∠FED,
∴∠HFE=∠FCD
∴EF∥CD
∴四边形CDEF是平行四边形,
又CD=DE
∴四边形CDEF是菱形(有一组邻边相等的平行四边形是菱形)
∵△ABC中,∠ACB=90°,
∴DC⊥CB,
又∵DE⊥AB于E,且∠ABC的平分线BD交AC于点D,
∴CD=DE(角平分线上的点到角的两边的距离相等)
在△CBD与△EBD中,
|
∴△CBD≌△EBD
∴∠CDF=∠EDF
又在△CDF与△EDF中,
|
∴△CDF≌△EDF
∴∠FCD=∠FED
又CH⊥AB于H,且交BD于点F,DE⊥AB于E,
∴CF∥DE,∠HFE=∠FED,
∴∠HFE=∠FCD
∴EF∥CD
∴四边形CDEF是平行四边形,
又CD=DE
∴四边形CDEF是菱形(有一组邻边相等的平行四边形是菱形)
看了 如图所示,△ABC中,∠AC...的网友还看了以下:
在一四棱锥P-ABCD中,低面ABCD是正方形,侧棱PA垂直底面ABCD,PA=AD=1,E为AC 2020-04-11 …
如图,一个匀速转动的圆盘上有a、b、c三点,已知,则下面说法中错误的()A、a、b、c三点的角速度 2020-05-21 …
如图1,在矩形ABCD中,AB=4,AD=2,点P是边AB上的一个动点(不与点A、点B重合),点Q 2020-06-22 …
一个边长为1的正方体,一只蚂蚁在A点,它需要到相对的F点觅食,它从A点到F点的最短距离是多少? 2020-07-03 …
如图为一小球从A点沿直线运动到F点的频闪照片,若频闪照相机每隔0.2s闪拍一次,分析照片可知:小球 2020-07-20 …
如图所示,是一个小球从A点沿直线运动到F的频闪照片,若频闪照相机没隔0.2s闪拍一次.分析照片可知 2020-07-22 …
(2013•婺城区一模)如图1,在矩形ABCD中,AB=4,AD=2,点P是边AB上的一个动点(不与 2020-11-01 …
(2014•安顺)如图是一小球从A点沿直线运动到F点的频闪照片,若频闪照相机每隔0.2s闪拍一次,分 2020-11-13 …
如图所示,有一对等量异种电荷分别位于空间中的a点和f点,以a点和f点为顶点作一正立方体.现在各顶点间 2020-12-01 …
如图1,在矩形ABCD中,AB=4,AD=2,点P是边AB上的一个动点(不与点A、点B重合),点Q在 2020-12-25 …