两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB，在探究筝形的性质时，得到如下结论：①△ABD≌△CBD；②AC⊥BD；③四边形ABCD的面积=12AC•BD，其中

Question

两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB，在探究筝形的性质时，得到如下结论：①△ABD≌△CBD；②AC⊥BD；③四边形ABCD的面积=

(1)/(2)AC•BD，其中正确的结论有（　　）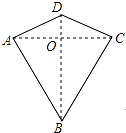

A. 0个

B. 1个

C. ．2个

D. ．3个

Answer 1

在△ABD与△CBD中，

AD=CD

AB=BC

DB=DB

，
∴△ABD≌△CBD（SSS），
故①正确；
∴∠ADB=∠CDB，
在△AOD与△COD中，

AD=CD

∠ADB=∠CDB

OD=OD

，
∴△AOD≌△COD（SAS），
∴∠AOD=∠COD=90°，AO=OC，
∴AC⊥DB，
故②正确；
四边形ABCD的面积=S△ADB+S△BDC=(1)/(2)DB×OA+(1)/(2)DB×OC=(1)/(2)AC•BD，
故③正确；
故选D．