早教吧作业答案频道 -->数学-->
对于一个四边形给出如下定义:有一组对角相等且有一组邻边相等,则称这个四边形为奇特四边形.(1)判断命题“另一组邻边也相等的四边形为正方形”是真命题还是假命题?(2)如图
题目详情
对于一个四边形给出如下定义:有一组对角相等且有一组邻边相等,则称这个四边形为奇特四边形.
(1)判断命题“另一组邻边也相等的四边形为正方形”是真命题还是假命题?
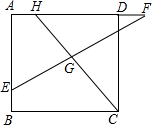
(2)如图,在正方形ABCD中,E为AB边上一点,F是AD延长线一点,BE=DF,连接EF,取EF的中点G,连接CG并延长交AD于点H,探究:四边形BCGE是否是奇特四边形,如果是,请证明你的结论;如果不是,请说明理由.
(3)在(2)的条件下,若四边形BCGE的面积是16,设BC=x,BE=y,
①求x+y的值;
②求当x+xy取最大值时FH的长.

(1)判断命题“另一组邻边也相等的四边形为正方形”是真命题还是假命题?
(2)如图,在正方形ABCD中,E为AB边上一点,F是AD延长线一点,BE=DF,连接EF,取EF的中点G,连接CG并延长交AD于点H,探究:四边形BCGE是否是奇特四边形,如果是,请证明你的结论;如果不是,请说明理由.
(3)在(2)的条件下,若四边形BCGE的面积是16,设BC=x,BE=y,
①求x+y的值;
②求当x+xy取最大值时FH的长.
▼优质解答
答案和解析
(1)假命题,如图,AB=AC,∠ABD=∠ACD,又DC=DB,明显四边形ABDC不是正方形.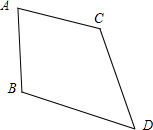
(2)连接CE,CF∵四边形ABCD是正方形,
∴BC=DC,∠EBC=∠FDC=90°,
在△EBC和△FDC中,
∴△CBE≌△CDF(SAS)
∴CE=CF,∠BCE=∠DCE
∴∠ECF=90°,
∵G是EF的中点,
∴GE=GC,∠EGC=90°,
∵GE=GC,∠EGC=∠B=90°
∴四边形BCGE是奇特四边形;
(3)①过点G作MN∥AB,GQ∥AD,
∴△GQE≌△GMC(AAS)
∴GQ=GM,
∴四边形BMGQ是正方形,S四边形BCGE=S正方形BMGQ,
∵四边形BCGE的面积是16,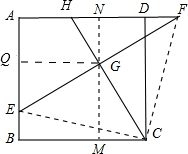
∴S正方形BMGQ=16
∴GQ=GM=AN=4,
∵G是EF的中点,
∴AN=FN=4,
∴AF=8
∵BE=DF,BC=AD,
∴BE+BC=AF=8
∵BC=x,BE=y
∴x+y=8;
②由①知y=8-x,
∴x+xy=x+x(8-x)=-x2+9x=-(x-
)2+
,
∴x+xy取最大值时,x=BC=4.5,y=BE=3.5
∴CE=CF=
=
,
∴FG=
∵Rt△FGH∽Rt△FNG
∴FG2=FN•FH
∵FN=4,FG=
,
∴FH=
.

(2)连接CE,CF∵四边形ABCD是正方形,
∴BC=DC,∠EBC=∠FDC=90°,
在△EBC和△FDC中,
|
∴△CBE≌△CDF(SAS)
∴CE=CF,∠BCE=∠DCE
∴∠ECF=90°,
∵G是EF的中点,
∴GE=GC,∠EGC=90°,
∵GE=GC,∠EGC=∠B=90°
∴四边形BCGE是奇特四边形;
(3)①过点G作MN∥AB,GQ∥AD,
∴△GQE≌△GMC(AAS)
∴GQ=GM,
∴四边形BMGQ是正方形,S四边形BCGE=S正方形BMGQ,
∵四边形BCGE的面积是16,

∴S正方形BMGQ=16
∴GQ=GM=AN=4,
∵G是EF的中点,
∴AN=FN=4,
∴AF=8
∵BE=DF,BC=AD,
∴BE+BC=AF=8
∵BC=x,BE=y
∴x+y=8;
②由①知y=8-x,
∴x+xy=x+x(8-x)=-x2+9x=-(x-
| 9 |
| 2 |
| 81 |
| 4 |
∴x+xy取最大值时,x=BC=4.5,y=BE=3.5
∴CE=CF=
(
|
| ||
| 2 |
∴FG=
| ||
| 4 |
∵Rt△FGH∽Rt△FNG
∴FG2=FN•FH
∵FN=4,FG=
| ||
| 4 |
∴FH=
| 65 |
| 16 |
看了 对于一个四边形给出如下定义:...的网友还看了以下:
读长江流域水系图,回答17-18题.以下有关长江各河段的表述,正确的是()A.甲河段多峡谷险滩,落 2020-04-06 …
根据下面的两种移动电话计费方式表,考虑下列问题.方式1方式2月租费30元/月0本地通话费0.30元 2020-06-04 …
(2014•宜昌)物质除杂是化学实验中经常遇到的问题.方法探究为了除去二氧化碳气体中混有的少量一氧 2020-06-12 …
如图是一游客在列车上拍摄的西藏太阳能发电的景观图片,图中的箭头表示列车行进方向.读后回答3-4题. 2020-06-15 …
图中的虚线圈是正常情况下发生在赤道附近太平洋洋面上的一种热力环流.回答7、8题.以下关于该环流中气 2020-06-22 …
读图,完成19~20题.以下关于长江沿岸开发利用与保护方式较合理的是()A.上游-----伐林垦草 2020-06-24 …
读图,完成19-20小题.以下关于长江沿岸开发利用与保护方式较合理的是()A.上游----伐林垦草 2020-06-27 …
某研究性学习小组为证明2Fe3++2I-⇌2Fe2++I2为可逆反应(即反应存在一定的限度),设计 2020-07-04 …
出门在外,看路牌,辨方向,好行路.外地人小杨开车到长泰县城,在靠近某一个路口时看到右下图所示的路牌 2020-07-05 …
为测定碳酸氢钠纯度(含有少量氯化钠),学生设计了如下几个实验方案(每个方案均称取m1g样品),请回 2020-07-28 …