早教吧作业答案频道 -->数学-->
如图,已知抛物线y=-14x2-12x+2与x轴交于A、B两点,与y轴交于点C(1)求点A,B,C的坐标;(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;(3)
题目详情
如图,已知抛物线y=-
x2-
x+2与x轴交于A、B两点,与y轴交于点C
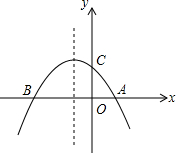
(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
| 1 |
| 4 |
| 1 |
| 2 |

(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
▼优质解答
答案和解析
(1)令y=0得-
x2-
x+2=0,
∴x2+2x-8=0,
x=-4或2,
∴点A坐标(2,0),点B坐标(-4,0),
令x=0,得y=2,∴点C坐标(0,2).
(2)由图象①AB为平行四边形的边时,
∵AB=EF=6,对称轴x=-1,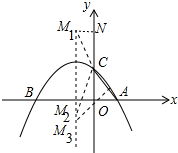
∴点E的横坐标为-7或5,
∴点E坐标(-7,-
)或(5,-
),此时点F(-1,-
),
∴以A,B,E,F为顶点的平行四边形的面积=6×
=
.
②当点E在抛物线顶点时,点E(-1,
),设对称轴与x轴交点为M,令EM与FM相等,则四边形AEBF是菱形,此时以A,B,E,F为顶点的平行四边形的面积=
×6×
=
.
(3)如图所示,①当C为顶点时,CM1=CA,CM2=CA,作M1N⊥OC于N,
在RT△CM1N中,CN=
=
,
∴点M1坐标(-1,2+
),点M2坐标(-1,2-
).
②当M3为顶点时,∵直线AC解析式为y=-x+2,
线段AC的垂直平分线为y=x,
∴点M3坐标为(-1,-1).
③当点A为顶点的等腰三角形不存在.
综上所述点M坐标为(-1,-1)或(-1,2+
)或(-1,2-
).
| 1 |
| 4 |
| 1 |
| 2 |
∴x2+2x-8=0,
x=-4或2,
∴点A坐标(2,0),点B坐标(-4,0),
令x=0,得y=2,∴点C坐标(0,2).
(2)由图象①AB为平行四边形的边时,
∵AB=EF=6,对称轴x=-1,

∴点E的横坐标为-7或5,
∴点E坐标(-7,-
| 27 |
| 4 |
| 27 |
| 4 |
| 27 |
| 4 |
∴以A,B,E,F为顶点的平行四边形的面积=6×
| 27 |
| 4 |
| 81 |
| 2 |
②当点E在抛物线顶点时,点E(-1,
| 9 |
| 4 |
| 1 |
| 2 |
| 9 |
| 2 |
| 27 |
| 2 |
(3)如图所示,①当C为顶点时,CM1=CA,CM2=CA,作M1N⊥OC于N,
在RT△CM1N中,CN=
| CM12-M1N2 |
| 7 |
∴点M1坐标(-1,2+
| 7 |
| 7 |
②当M3为顶点时,∵直线AC解析式为y=-x+2,
线段AC的垂直平分线为y=x,
∴点M3坐标为(-1,-1).
③当点A为顶点的等腰三角形不存在.
综上所述点M坐标为(-1,-1)或(-1,2+
| 7 |
| 7 |
看了 如图,已知抛物线y=-14x...的网友还看了以下:
220kV及以上变压器新油电气绝缘强度为( )kV。 A.30以上 B.35以上 C.40以上 D. 2020-05-31 …
室内紫外线杀菌的适宜温、湿度是A.20℃以下,30%以上B.20℃以下,50%以上C.20℃以上,4 2020-06-07 …
肠鸣音亢进是指肠鸣音每分钟超过A.4次以上B.5次以上C.6次以上D.8次以上E.10次以上 2020-06-07 …
如图中a,b,c表示生物体内的三个生理过程,其中的Y分别代表三种物质,有关Y的叙述,错误的是()A 2020-06-13 …
已知点P的横坐标为A,纵坐标为0,则点P在()A.x轴上B.y轴上C.第一,三象限或第二,四象限内 2020-06-21 …
已知点P(x,y),如果x^2+y^2=0,那么点P的位置在?A.x轴上B.y轴上C.x轴或y轴上 2020-07-30 …
已知点B(m,n),且m+n等于0,则点B在?A.x轴上B.y轴上C.位置无法确定D.第二、第四象 2020-08-03 …
读我国某地1月等温线分布图,判断图中①②两地的气温()A.①处在0℃以上,②处在4℃以上B.①处在0 2020-11-02 …
已知106x+64y=z,求z为几时以上数字x,y整数106x+64y=zz为85,90,95,10 2020-11-18 …
关于岩石圈她叙述,正确她是()A.位于地面以下,古登堡界面以上B.位于地面以下,莫霍界面以上C.位于 2020-11-21 …