如图△ABC中底边BC＝12，其它两边AB和AC上中线的和为30，求此三角形重心G的轨迹方程，并求顶点A的轨迹方程．

Question

如图△ABC中底边BC＝12，其它两边AB和AC上中线的和为30，求此三角形重心G的轨迹方程，并求顶点A的轨迹方程．

Answer 1

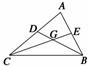
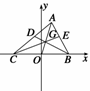
解　以BC边所在直线为x轴，BC边中点为原点，建立如图所示坐标系，

则B(6 0)，C(－6 0)，CE、BD为AB、AC边上的中线，则|BD|＋|CE|＝30.

由重心性质可知

|GB|＋|GC|

＝(|BD|＋|CE|)＝20.

∵B、C是两个定点，G点到B、C距离和等于定值20，且20>12，

∴G点的轨迹是椭圆，B、C是椭圆焦点．

∴2c＝|BC|＝12，c＝6 2a＝20，a＝10，

b²＝a²－c²＝10²－6²＝64，

故G点的轨迹方程为＋＝1 (x≠±10)．

又设G(x′，y′)，A(x，y)，则有＋＝1.

由重心坐标公式知

故A点轨迹方程为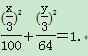

即＋＝1 (x≠±30)．