早教吧作业答案频道 -->数学-->
如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC.(1)求证:直线DM是⊙O的切线;(2)求证:DE2=DF•DA.
题目详情
如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC.
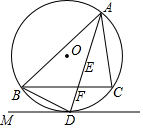
(1)求证:直线DM是⊙O的切线;
(2)求证:DE2=DF•DA.

(1)求证:直线DM是⊙O的切线;
(2)求证:DE2=DF•DA.
▼优质解答
答案和解析
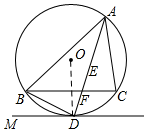 (1)如图所示,连接OD,
(1)如图所示,连接OD,
∵点E是△ABC的内心,
∴∠BAD=∠CAD,
∴
=
,
∴OD⊥BC,
又∵∠BDM=∠DAC,∠DAC=∠DBC,
∴∠BDM=∠DBC,
∴BC∥DM,
∴OD⊥DM,
∴直线DM是⊙O的切线;
(2)如图所示,连接BE,
∵点E是△ABC的内心,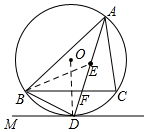
∴∠BAE=∠CAE=∠CBD,∠ABE=∠CBE,
∴∠BAE+∠ABE=∠CBD+∠CBE,
即∠BED=∠EBD,
∴DB=DE,
∵∠DBF=∠DAB,∠BDF=∠ADB,
∴△DBF∽△DAB,
∴
=
,即DB2=DF•DA,
∴DE2=DF•DA.
 (1)如图所示,连接OD,
(1)如图所示,连接OD,∵点E是△ABC的内心,
∴∠BAD=∠CAD,
∴
 |
| BD |
 |
| CD |
∴OD⊥BC,
又∵∠BDM=∠DAC,∠DAC=∠DBC,
∴∠BDM=∠DBC,
∴BC∥DM,
∴OD⊥DM,
∴直线DM是⊙O的切线;
(2)如图所示,连接BE,
∵点E是△ABC的内心,

∴∠BAE=∠CAE=∠CBD,∠ABE=∠CBE,
∴∠BAE+∠ABE=∠CBD+∠CBE,
即∠BED=∠EBD,
∴DB=DE,
∵∠DBF=∠DAB,∠BDF=∠ADB,
∴△DBF∽△DAB,
∴
| DF |
| DB |
| DB |
| DA |
∴DE2=DF•DA.
看了 如图,点E是△ABC的内心,...的网友还看了以下:
已知双曲线的中心在原点,右顶点A(1,0),点P、Q在双曲线的右支上,点M[5-2根号2,0到直线的 2020-03-31 …
初中数学竞赛几何证明题已知点o为等边三角形ABC的内心,直线m过点o,过A、B、C三点分别作直线m 2020-05-16 …
已知平面α与平面β相交,直线m⊥α,则()A.β内必存在直线与m平行,且存在直线与m垂直B.β内不 2020-05-24 …
(2014•龙东地区)已知△ABC中,M为BC的中点,直线m绕点A旋转,过B、M、C分别作BD⊥m 2020-06-15 …
已知直线m,n相交于点B,点A,C分别为直线m,n上的点,AB=BC=1,且∠ABC=60°,点E 2020-06-19 …
已知动圆P过定点A(-3,0),并且与定圆B:(x-3)2+y2=64内切.(1)求动圆圆心P的轨 2020-07-20 …
两个平面α与β相交但不垂直,直线m在平面α内,则在平面β内()A.一定存在与直线m平行的直线B.一 2020-07-25 …
下列命题正确的是()A.若a是平面M的斜线,b垂直于a在平面M内的射影,则a⊥bB.若a是平面M的 2020-07-30 …
下列命题中正确的命题是()A.若a是平面M的斜线直线b垂直于a在M内的射影则a⊥bB.若a是平面M 2020-07-30 …
(1).在三角形ABC中角BAC等于90度,AB等于AC,直线m经过A,BD垂直m,CE垂直m,垂足 2020-12-25 …