早教吧作业答案频道 -->数学-->
如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.(1)求证:DB=DE;(2)求证:直线CF为⊙O的切线.
题目详情
如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.
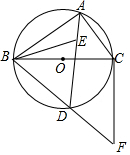
(1)求证:DB=DE;
(2)求证:直线CF为⊙O的切线.

(1)求证:DB=DE;
(2)求证:直线CF为⊙O的切线.
▼优质解答
答案和解析
(1)证明:∵E是△ABC的内心,
∴∠BAE=∠CAE,∠EBA=∠EBC,
∵∠BED=∠BAE+∠EBA,∠DBE=∠EBC+∠DBC,∠DBC=∠EAC,
∴∠DBE=∠DEB,
∴DB=DE.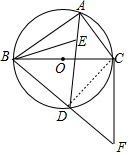
(2)连接CD.
∵DA平分∠BAC,
∴∠DAB=∠DAC,
∴
=
,
∴BD=CD,
∵BD=DF,
∴CD=DB=DF,
∴∠BCF=90°,
∴BC⊥CF,
∴CF是⊙O的切线.
∴∠BAE=∠CAE,∠EBA=∠EBC,
∵∠BED=∠BAE+∠EBA,∠DBE=∠EBC+∠DBC,∠DBC=∠EAC,
∴∠DBE=∠DEB,
∴DB=DE.

(2)连接CD.
∵DA平分∠BAC,
∴∠DAB=∠DAC,
∴
 |
| BD |
 |
| CD |
∴BD=CD,
∵BD=DF,
∴CD=DB=DF,
∴∠BCF=90°,
∴BC⊥CF,
∴CF是⊙O的切线.
看了 如图,⊙O是△ABC的外接圆...的网友还看了以下:
化简下列逻辑函数①F=(A+B)C+AB②F=AC+AB+BC③F=ABC+ABC+ABC+ABC 2020-04-25 …
如何确定偏导数极值?例如:已知a,b,c是满足a^2=b^2+c^2的正数,求函数f(a,b,c) 2020-04-26 …
设在关系模式R(A,B,C,D,E,F,G)中,根据语义有如下函数依赖集F={A→B,C→D,C→F 2020-05-23 …
设在关系模式R(A,B,C,D,E,F,G)中,根据语义有如下函数依赖集F=(A→B,C→D,C→F 2020-05-23 …
设在关系模式R(A,B,C,D,E,F,G)中,根据语义有如下函数依赖集F=(A→B,C→D,C→F 2020-05-23 …
设有关系模式R(A,B,C,D,E,F,G),根据语义有如下函数依赖集F={A→B,C→D,C→F, 2020-05-23 …
设有关系模式R(A,B,C,D,E,F),若有如下的函数依赖集F={A→B,(C,A)→D, (E, 2020-05-24 …
关于java的swap比如有[a,b,c,d,e]5个字母...用swap交换为[d,e,c,a, 2020-07-17 …
设集合X={(a,b,c)|a,b,c属于Z},f是从X到X的映射,且满足f(a,b,c)=(a+ 2020-07-30 …
EXCEL循环或计算问题。F=A+B+C+D+E。(A.B.C.D.E.F.均要大于零)E=A*10 2020-11-01 …