早教吧作业答案频道 -->数学-->
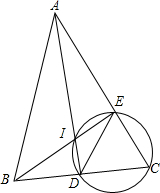
如图,若AD、BE为△ABC的两条角平分线,I为内心,若C,D,I,E四点共圆,且DE=1,则ID=.
题目详情
如图,若AD、BE为△ABC的两条角平分线,I为内心,若C,D,I,E四点共圆,且DE=1,则ID=___.

▼优质解答
答案和解析
连接CI,
∵AD、BE为△ABC的两条角平分线,
∴∠BAI=
∠BAC,∠IBA=
∠ABC,
∵∠AIB=180°-∠BAI-∠IBA,
∴∠AIB=180°-
(∠CAB+∠CBA),
又∵∠ABC+∠CBA+∠ACB=180°,
∴∠AIB=90°+
∠C,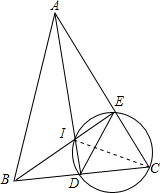
∵C,D,I,E四点共圆,
∴∠EID+∠ACB=180°,
又∵∠AIB=∠EID,
∴90°+
∠C+∠C=180°,
∴∠ACB=60°,
∵I为内心,
∴∠ICD=30°,
∵DE=1,
∴
=2R,
∴R=
,
∴
=2R,
∴ID=
,
故答案为:
.
∵AD、BE为△ABC的两条角平分线,
∴∠BAI=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AIB=180°-∠BAI-∠IBA,
∴∠AIB=180°-
| 1 |
| 2 |
又∵∠ABC+∠CBA+∠ACB=180°,
∴∠AIB=90°+
| 1 |
| 2 |

∵C,D,I,E四点共圆,
∴∠EID+∠ACB=180°,
又∵∠AIB=∠EID,
∴90°+
| 1 |
| 2 |
∴∠ACB=60°,
∵I为内心,
∴∠ICD=30°,
∵DE=1,
∴
| DE |
| sin60° |
∴R=
| ||
| 3 |
∴
| ID |
| sin30° |
∴ID=
| ||
| 3 |
故答案为:
| ||
| 3 |
看了 如图,若AD、BE为△ABC...的网友还看了以下:
党在社会主义初级阶段的基本路线概括为“一个中心,两个基本点”,“一个中心”是指()A.以坚持四项基 2020-04-22 …
中共十三大明确提出“一个中心,两个基本点”的基本路线,其中“一个中心”是指A.以改革开放为中心B. 2020-04-22 …
中共“十三大”明确提出了“一个中心,两个基本点”的基本路线,其中“一个中心”是指()A.以改革开放 2020-04-22 …
社会主义初级阶段的基本路线可以概括为“一个中心,两个基本点”,其中“一个中心”是()A.以阶级斗争 2020-04-22 …
党的基本路线的核心内容是“一个中心,两个基本点”,其中“一个中心”是指()A.以思想建设为中心B. 2020-05-14 …
信息系统建设也称为信息工程,在实施中应A.以数据为中心B.以应用为中心C.以业务为中心D.以技术为 2020-05-23 …
James Martin方法强调,信息系统开发应以A.应用为中心B.业务为中心C.数据为中心D.信息 2020-05-23 …
决策支持系统是以A.数据库为中心B.模型库为中心C.对话系统为中心D.知识表示为中心 2020-05-23 …
决策支持系统是以______。A.数据库为中心B.模型库为中心C.对话系统为中心D.知识表示为中心 2020-05-23 …
决策支持系统是以()。A.数据库为中心B.模型库为中心C.对话系统为中心D.知识表示为中心 2020-05-24 …