早教吧作业答案频道 -->数学-->
如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.(1)证明:AC1⊥A1B;(2)设二面角A1-AB-C的正切值为15.求直线AA1与平面BCC1B1的距离.
题目详情
如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.
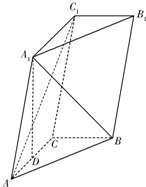
(1)证明:AC1⊥A1B;
(2)设二面角A1-AB-C的正切值为
.求直线AA1与平面BCC1B1的距离.

(1)证明:AC1⊥A1B;
(2)设二面角A1-AB-C的正切值为
| 15 |
▼优质解答
答案和解析
证明:(1)因为A1D⊥平面ABC,A1D⊂平面AA1C1C,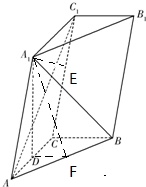
故平面AA1C1C⊥平面ABC,
又BC⊥AC,所以BC⊥平面AA1C1C,连接A1C.
因为侧面AA1C1C为菱形,故AC1⊥A1C.
由三垂线定理得AC1⊥A1B.
(2)BC⊥平面AA1C1C,BC⊂平面BCC1B1.
故平面AA1C1C⊥平面BCC1B1.
作A1E⊥CC1,E为垂足,则A1E⊥平面BCC1B1.
作DF⊥AB,F为垂足,连接A1F.
由三垂线定理得A1F⊥AB,
故∠A1FD为二面角A1-AB-C的平面角.
设AD=x则A1D=
,DF=
x,而tan∠A1FD=
=
,
故x=1,所以D是AC的中点,
故A1D=
为直线AA1与平面BCC1B1的距离.

故平面AA1C1C⊥平面ABC,
又BC⊥AC,所以BC⊥平面AA1C1C,连接A1C.
因为侧面AA1C1C为菱形,故AC1⊥A1C.
由三垂线定理得AC1⊥A1B.
(2)BC⊥平面AA1C1C,BC⊂平面BCC1B1.
故平面AA1C1C⊥平面BCC1B1.
作A1E⊥CC1,E为垂足,则A1E⊥平面BCC1B1.
作DF⊥AB,F为垂足,连接A1F.
由三垂线定理得A1F⊥AB,
故∠A1FD为二面角A1-AB-C的平面角.
设AD=x则A1D=
| 4-x2 |
| ||
| 5 |
| A1D |
| DF |
| 15 |
故x=1,所以D是AC的中点,
故A1D=
| 3 |
看了 如图,三棱柱ABC-A1B1...的网友还看了以下:
(1)A、B均为n阶实对称正定矩阵,证明A-B正定则B^(-1)-A^(-1)亦正定(2)A、(1 2020-05-13 …
边际消费倾向和边际储蓄倾向均为大于零而小于1的参数,且两者之和为1。( )A.正确B.错误 2020-05-21 …
所有者权益比率×资产负债率=1。()A.正确B.错误 2020-05-21 …
判定系数和调整后的判定系数的取值永远为正,且不大于1。()A.正确B.错误 2020-05-21 …
平均增长速度等于平均发展速度减1。()A.正确B.错误 2020-06-07 …
2.证明:(1)a,b为不等的正整数,1/a、1/b的算术平均值为1/6==>a、b的算术;2.证 2020-06-13 …
证明:(1)a,b为不等的正整数,1/a、1/b的算术平均值为1/6==>a;;证明:(1)a,b 2020-06-13 …
利息保障倍数不能低于1。A.正确B.错误 2020-06-27 …
排球理论题急、判断题:战术意识,一般是运动员在运动的时间中所具有的经验,才能与知识.(1分)A.正确 2020-10-30 …
①正实数x,y,满足2x+y+6=xy,则求xy的最小值?②正数a,b,c,则a+1/b,b+1/c 2020-11-19 …