三棱锥P-ABC中，底面△ABC满足BA=BC，∠ABC=π2，P在面ABC的射影为AC的中点，且该三棱锥的体积为92，当其外接球的表面积最小时，P到面ABC的距离为（）A.2B.3C.23D.33

Question

三棱锥P-ABC中，底面△ABC满足BA=BC，∠ABC=

(π)/(2)，P在面ABC的射影为AC的中点，且该三棱锥的体积为(9)/(2)，当其外接球的表面积最小时，P到面ABC的距离为（　　）

A. 2

B. 3

C. 2

√(3)

D. 3

√(3)

Answer 1

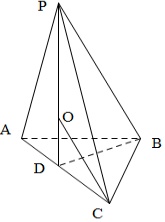设AC的中点为D，连接BD，PD，则PD⊥平面ABC，
∵△ABC是等腰直角三角形，∴外接球的球心O在PD上，
设AB=BC=a，PD=h，外接球半径OC=OP=R，
则OD=h-R，CD=(1)/(2)AC=(√(2))/(2)a，
∵V_P-ABC=(1)/(3)S△ABC•h=(1)/(3)•(1)/(2)a2•h=(9)/(2)，∴a²=(27)/(h)，
∵CD²+OD²=OC²，即（h-R）²+(1)/(2)a²=R²，
∴R=(h2+(1)/(2)a2)/(2h)=(h)/(2)+(27)/(4h2)=(h)/(4)+(h)/(4)+(27)/(4h2)≥3

3

(27)/(64)

=(9)/(4)，
当且仅当(h)/(4)=(h)/(4)=(27)/(4h2)即h=3时取等号，
∴当外接球半径取得最小值时，h=3．
故选：B．