早教吧作业答案频道 -->数学-->
(1)如图所示.在△ABC中,射影定理可表示为a=b•cosC+c•cosB.其中a,b,c分别为角A,B,C的对边,类比上述定理.写出对空间四面体性质的猜想.(2)已知在Rt△ABC中.AB⊥AC,AD⊥BC于D,
题目详情
(1)如图所示.在△ABC中,射影定理可表示为a=b•cosC+c•cosB.其中a,b,c分别为角A,B,C的对边,类比上述定理.写出对空间四面体性质的猜想.
(2)已知在Rt△ABC中.AB⊥AC,AD⊥BC于D,有
=
+
成立.那么在四面体A一BCD中,类比上述结论,你能得怎样的猜想,说明猜想是否正确并给出理由.
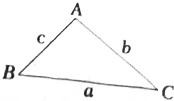
(2)已知在Rt△ABC中.AB⊥AC,AD⊥BC于D,有
| 1 |
| AD2 |
| 1 |
| AB2 |
| 1 |
| AC2 |

▼优质解答
答案和解析
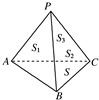 (1)如图,在四面体P-ABC中,S1、S2、S3、S分别表示△PAB、△PBC、△PCA、△ABC的面积,α、β、γ依次表示面PAB、面PBC、面PCA与底面ABC所成角的大小,我们猜想将射影定理类比推理到三维空间,其表现形式应为S=S1cosα+S2cosβ+S3cosγ,
(1)如图,在四面体P-ABC中,S1、S2、S3、S分别表示△PAB、△PBC、△PCA、△ABC的面积,α、β、γ依次表示面PAB、面PBC、面PCA与底面ABC所成角的大小,我们猜想将射影定理类比推理到三维空间,其表现形式应为S=S1cosα+S2cosβ+S3cosγ,
(2):类比AB⊥AC,AD⊥BC猜想:在四面体ABCD中,若AB⊥AC,AB⊥AD,AC⊥AD,AE⊥平面BCD,则
=
+
+
.
如图,连接BE交CD于F,连接AF.
∵AB⊥AC,AB⊥AD
∴AB⊥平面ACD.
而AF⊂平面ACD,∴AB⊥AF.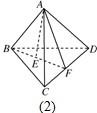
在Rt△ABF中,AE⊥BF,
∴
=
+
.
在Rt△ACD中,AF⊥CD,
∴
=
+
.
∴则
=
+
+
,
故猜想成立.
 (1)如图,在四面体P-ABC中,S1、S2、S3、S分别表示△PAB、△PBC、△PCA、△ABC的面积,α、β、γ依次表示面PAB、面PBC、面PCA与底面ABC所成角的大小,我们猜想将射影定理类比推理到三维空间,其表现形式应为S=S1cosα+S2cosβ+S3cosγ,
(1)如图,在四面体P-ABC中,S1、S2、S3、S分别表示△PAB、△PBC、△PCA、△ABC的面积,α、β、γ依次表示面PAB、面PBC、面PCA与底面ABC所成角的大小,我们猜想将射影定理类比推理到三维空间,其表现形式应为S=S1cosα+S2cosβ+S3cosγ,(2):类比AB⊥AC,AD⊥BC猜想:在四面体ABCD中,若AB⊥AC,AB⊥AD,AC⊥AD,AE⊥平面BCD,则
| 1 |
| AE2 |
| 1 |
| AB2 |
| 1 |
| AC2 |
| 1 |
| AD2 |
如图,连接BE交CD于F,连接AF.
∵AB⊥AC,AB⊥AD
∴AB⊥平面ACD.
而AF⊂平面ACD,∴AB⊥AF.

在Rt△ABF中,AE⊥BF,
∴
| 1 |
| AE2 |
| 1 |
| AB2 |
| 1 |
| AF2 |
在Rt△ACD中,AF⊥CD,
∴
| 1 |
| AF2 |
| 1 |
| AC2 |
| 1 |
| AD2 |
∴则
| 1 |
| AE2 |
| 1 |
| AB2 |
| 1 |
| AC2 |
| 1 |
| AD2 |
故猜想成立.
看了 (1)如图所示.在△ABC中...的网友还看了以下:
先读懂古诗,然后回答诗中问题.巍巍古寺在山林,不知寺内几多僧.三百六十四只碗,看看用尽不差争.三人共 2020-03-31 …
先读懂古诗,然后回答诗中问题.巍巍古寺在山林,不知寺内几多僧.三百六十四只碗,看看用尽不差争.三人共 2020-03-31 …
先读懂古诗,然后回答诗中问题.巍巍古寺在山林,不知寺内几多僧.三百六十四只碗,看看用尽不差争.三人共 2020-03-31 …
先读懂古诗,然后回答诗中问题.巍巍古寺在山林,不知寺内几多僧.三百六十四只碗,看看用尽不差争.三人 2020-04-27 …
先读懂古诗,然后回答诗中问题.巍巍古寺在山林,不知寺内几多僧.三百六十四只碗,看看用尽不差争.三人 2020-05-20 …
先读懂古诗,然后回答诗中问题.巍巍古寺在山林,不知寺内几多僧.三百六十四只碗,看看用尽不差争.三人 2020-05-20 …
先读懂古诗,然后回答诗中问题.巍巍古寺在山林,不知寺内几多僧.三百六十四只碗,看看用尽不差争.三人 2020-05-20 …
先读懂古诗,然后回答诗中问题.巍巍古寺在山林,不知寺内几多僧.三百六十四只碗,看看用尽不差争.三人 2020-05-20 …
先读懂古诗,然后回答诗中问题.巍巍古寺在山林,不知寺内几多僧.三百六十四只碗,看看用尽不差争.三人 2020-06-03 …
如图中S为发光点,从它发出的两条光线经平面镜反射后的两条反射光线分别与虚线a、b重合,根据平面镜成 2020-07-05 …