早教吧作业答案频道 -->数学-->
如图,O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交O于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF.(1)若∠POC=60°,AC=12,求劣弧PC的长;(结果保留π)
题目详情
如图, O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交 O于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF.
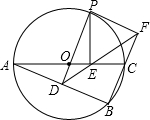
(1)若∠POC=60°,AC=12,求劣弧PC的长;(结果保留π)
(2)求证:OD=OE;
(3)求证:PF是 O的切线.

(1)若∠POC=60°,AC=12,求劣弧PC的长;(结果保留π)
(2)求证:OD=OE;
(3)求证:PF是 O的切线.
▼优质解答
答案和解析
(1) ∵AC=12,
∴CO=6,
∴
=
=2π;
答:劣弧PC的长为:2π.
(2)证明:∵PE⊥AC,OD⊥AB,
∠PEA=90°,∠ADO=90°
在△ADO和△PEO中,
,
∴△POE≌△AOD(AAS),
∴OD=EO;
(3)证明:
法一:
如图,连接AP,PC,
∵OA=OP,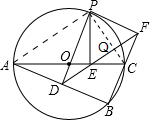
∴∠OAP=∠OPA,
由(2)得OD=EO,
∴∠ODE=∠OED,
又∵∠AOP=∠EOD,
∴∠OPA=∠ODE,
∴AP∥DF,
∵AC是直径,
∴∠APC=90°,
∴∠PQE=90°
∴PC⊥EF,
又∵DP∥BF,
∴∠ODE=∠EFC,
∵∠OED=∠CEF,
∴∠CEF=∠EFC,
∴CE=CF,
∴PC为EF的中垂线,
∴∠EPQ=∠QPF,
∵△CEP∽△CAP
∴∠EPQ=∠EAP,
∴∠QPF=∠EAP,
∴∠QPF=∠OPA,
∵∠OPA+∠OPC=90°,
∴∠QPF+∠OPC=90°,
∴OP⊥PF,
∴PF是 O的切线.
法二:
设 O的半径为r.
∵OD⊥AB,∠ABC=90°,
∴OD∥BF,∴△ODE≌△CFC
又∵OD=OE,∴FC=EC=r-OE=r-OD=r-
BC
∴BF=BC+FC=r+
BC
∵PD=r+OD=r+
BC
∴PD=BF
又∵PD∥BF,且∠DBF=90°,
∴四边形DBFP是矩形
∴∠OPF=90°
OP⊥PF,
∴PF是 O的切线.
∴CO=6,
∴
 |
| PC |
| 60•π•6 |
| 180 |
答:劣弧PC的长为:2π.
(2)证明:∵PE⊥AC,OD⊥AB,
∠PEA=90°,∠ADO=90°
在△ADO和△PEO中,
|
∴△POE≌△AOD(AAS),
∴OD=EO;
(3)证明:
法一:
如图,连接AP,PC,
∵OA=OP,

∴∠OAP=∠OPA,
由(2)得OD=EO,
∴∠ODE=∠OED,
又∵∠AOP=∠EOD,
∴∠OPA=∠ODE,
∴AP∥DF,
∵AC是直径,
∴∠APC=90°,
∴∠PQE=90°
∴PC⊥EF,
又∵DP∥BF,
∴∠ODE=∠EFC,
∵∠OED=∠CEF,
∴∠CEF=∠EFC,
∴CE=CF,
∴PC为EF的中垂线,
∴∠EPQ=∠QPF,
∵△CEP∽△CAP
∴∠EPQ=∠EAP,
∴∠QPF=∠EAP,

∴∠QPF=∠OPA,
∵∠OPA+∠OPC=90°,
∴∠QPF+∠OPC=90°,
∴OP⊥PF,
∴PF是 O的切线.
法二:
设 O的半径为r.
∵OD⊥AB,∠ABC=90°,
∴OD∥BF,∴△ODE≌△CFC
又∵OD=OE,∴FC=EC=r-OE=r-OD=r-
| 1 |
| 2 |
∴BF=BC+FC=r+
| 1 |
| 2 |
∵PD=r+OD=r+
| 1 |
| 2 |
∴PD=BF
又∵PD∥BF,且∠DBF=90°,
∴四边形DBFP是矩形
∴∠OPF=90°
OP⊥PF,
∴PF是 O的切线.
看了 如图,O是△ABC的外接圆,...的网友还看了以下:
今晚7.00之前给我!靓男靓女来看看~1用36米长的篱笆围城一个长方形菜地,要求宽是长的五分之四. 2020-05-13 …
用一根长为60厘米的铁丝按要求围成一个图形【其他内容在补充里】{1}如果要求围成一个长方形,使长方 2020-05-17 …
以下关于仪表PID整定的说法不正确的是( )。A、如果是长周期震荡(数倍于位式调节时震荡周期),可 2020-05-31 …
计算长方体的体积公式是什么其中,长×宽求的是长方体什么的面积,宽x高求的是什么面积 2020-06-02 …
30米0.2*0.25MM的铁络丝有多大功率?如果是长度为30米,0.2*0.25MM(宽乘厚)的 2020-06-05 …
一个长方形的宽是长的5\8,如果宽增加7厘米,长减少5厘米,这个长方形就变成了正方形,求原来长方形 2020-06-06 …
弦长公式的2r*sin(θ/2)中的θ是弧度还是角度还有已知弦长供高求半径弧长还有求供高的公式需要 2020-06-20 …
非预期性支出导致的借款需求都是长期的。( )A.正确B.错误 2020-06-27 …
英语音标的问题,..比如mi:n我是读“咪嗯”还是“民”的第四声?ainounein我该怎么读?如 2020-06-29 …
有什么藤蔓型的水果?就是水果是长在藤蔓上的?有哪些常见的?求介绍! 2020-07-02 …