画出任一矩形ABCD的最小覆盖圆，画一个矩形ABCD中，AB=2cm，BC=4cm，若两个等圆完全覆盖这个矩形，请求出这两个等圆的最小半径．

Question

画出任一矩形ABCD的最小覆盖圆，画一个矩形ABCD中，AB=2cm，BC=4cm，若两个等圆完全覆盖这个矩形，请求出这两个等圆的最小半径．

Answer 1

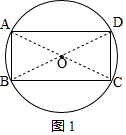
任意矩形ABCD的最下覆盖圆如图1所示， O即为所求；

如图2，AB=2cm，BC=4cm，

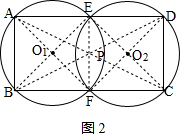
分别连接AC、BD，交于点P，
∴AP=PC，
过点P作EF⊥AD于点E，交BC于点F，
∴PE∥CD，
则AE=DE=AB=2cm，
∴四边形ABFE是正方形，
连接BE、AF交于点O₁，连接DF、CE交于点O₂，
分别以O₁、O₂为圆心，O₁A、O₂D为半径画圆，
则O₁A=O₁B=(√(2))/(2)AB=√(2)cm，
即这两个等圆的最小半径为√(2)cm．